题目内容
2.下列命题是真命题的是( )| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 对角线相等且互相垂直的四边形是正方形 | |
| C. | 若三角形的三边a、b、c满足a2+b2+c2=ac+bc+ab,则该三角形是正三角形 | |
| D. | 平分弦的直径垂直于弦,并且平分弦所对的弧 |
分析 利用平行线的性质、正方形的判定方法、配方法、成绩定理的推论进行判断即可.
解答 解:过直线外一点有且只有一条直线与已知直线平行,选项A是假命题;
对角线相等且互相垂直平分的四边形是正方形,选项B是假命题;
若三角形的三边a、b、c满足a2+b2+c2=ac+bc+ab,则该三角形是正三角形,是真命题;
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧,选项D是假命题;
故选:C.
点评 本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.

练习册系列答案
相关题目
13. 如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )
如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )
 如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )
如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{4}$ |
10.下列计算正确的是( )
| A. | (2x2)3=2x5 | B. | $\sqrt{6}$÷$\sqrt{3}$=2 | C. | 3a2+2a=5a3 | D. | 2m•5n=10mn |
7.计算$\sqrt{2}$sin30°+tan60°-cos45°的结果是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$-$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
14.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果盈利50元记作+50元,那么亏本30元记作:( )
| A. | -30元 | B. | -50元 | C. | +50元 | D. | +30元 |
11.抛物线y=-(x+2)2+6的对称轴是( )
| A. | x=-2 | B. | x=2 | C. | x=-6 | D. | x=6 |
12.与平面直角坐标系中的点具有一一对应关系的是( )
| A. | 实数 | B. | 有理数 | C. | 有序实数对 | D. | 有序有理数对 |
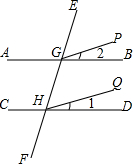 如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么?
如图,已知GP平分∠EGB,HQ平分∠GHD,如果∠1=∠2,那么GP∥HQ吗?为什么?