题目内容
13. 如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )
如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则∠OAB的正切值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{4}$ |
分析 作辅助线;首先证明△BOM∽△OAN,得到$\frac{BM}{ON}$=$\frac{OM}{AN}$,设B(-m,$\frac{1}{m}$),A(n,$\frac{2}{n}$),得到BM=$\frac{1}{m}$,AN=$\frac{2}{n}$,OM=m,ON=n,进而得到mn=$\frac{2}{mn}$,mn=$\sqrt{2}$,运用三角函数的定义证明知tan∠OAB=$\frac{\sqrt{2}}{2}$.
解答 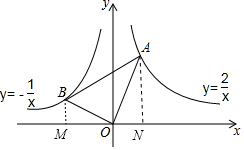 解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴$\frac{BM}{ON}$=$\frac{OM}{AN}$;
设B(-m,$\frac{1}{m}$),A(n,$\frac{2}{n}$),
则BM=$\frac{1}{m}$,AN=$\frac{2}{n}$,OM=m,ON=n,
∴mn=$\frac{2}{mn}$,mn=$\sqrt{2}$;
∵∠AOB=90°,
∴tan∠OAB=$\frac{OB}{OA}$①;
∵△BOM∽△OAN,
∴$\frac{OB}{OA}$=$\frac{BM}{ON}$=$\frac{1}{mn}$=$\frac{\sqrt{2}}{2}$②,
由①②知tan∠OAB=$\frac{\sqrt{2}}{2}$,
故选B.
点评 本题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
8.下列实数中,是无理数的为( )
| A. | $\frac{2}{3}$ | B. | 0 | C. | $\sqrt{36}$ | D. | -π |
5.若sin(α-10o)=$\frac{{\sqrt{3}}}{2}$,则∠α为( )
| A. | 30° | B. | 40° | C. | 60° | D. | 70° |
2.下列命题是真命题的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 对角线相等且互相垂直的四边形是正方形 | |
| C. | 若三角形的三边a、b、c满足a2+b2+c2=ac+bc+ab,则该三角形是正三角形 | |
| D. | 平分弦的直径垂直于弦,并且平分弦所对的弧 |
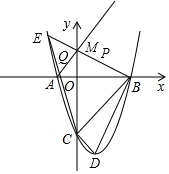 如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.
如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.