题目内容
12．在△ABC中，若点D为AB中点，点E是AC上一点，则下列条件能判断线段DE一定为△ABC中位线的是（ ）| A． | DE⊥AC | B． | CE=2AE | ||
| C． | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=1 | D． | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=$\frac{1}{3}$ |
分析 可先假设DE∥BC，由三角形中位线定理进而可得出结论．
解答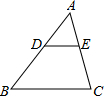 
解：根据题意可假设DE∥BC，则可得△ADE∽△ABC，
∵点D为AB中点，DE∥BC，
∴DE是△ABC中位线，
∴$\frac{AD}{AB}=\frac{1}{2}$，
∴$\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}=\frac{1}{3}$，
故选D．
点评 本题主要考查了由三角形中位线定理来判定两条直线平行线的问题，能够熟练掌握三角形中位线定理是解题关键．
练习册系列答案
相关题目
证明：三角形中位线定理．
20．下列判断正确的是（ ）
| A． | “任意选择某一电视频道，它正在播放动画片”是必然事件 | |
| B． | 某运动员投一次篮，投中的概率为0.8，则该运动员投5次篮，一定有4次投中 | |
| C． | 任总抛掷一枚均匀的硬币，反面朝上的概率为$\frac{1}{2}$ | |
| D． | 布袋里有3个白球，1个黑球．任意取出1个球，恰好是黑球的概率是$\frac{1}{3}$ |
7．若多项式m2-2m的值为2，则多项式2m2-4m-1的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
17．下列说法不正确的是（ ）
| A． | 为了解全市中学生对常州青果巷的知晓度的情况，适合用抽样调查 | |
| B． | 若甲组数据方差S甲2=0.39，乙组数据方差S乙2=0.27，则乙组数据比甲组数据稳定 | |
| C． | 某种彩票中奖的概率是$\frac{1}{100}$，买100张该种彩票一定会中奖 | |
| D． | 数据-1，1.5，2，2，4的中位数是2 |
4．
如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=70°，则∠B的度数为（ ）
如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=70°，则∠B的度数为（ ）| A． | 55° | B． | 60° | C． | 70° | D． | 75° |
