题目内容
1.如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.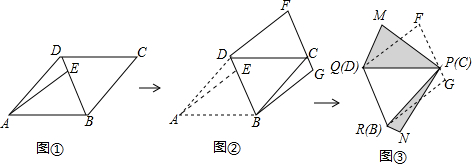
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为$\frac{6\sqrt{10}}{5}$.
分析 根据平移和翻折的性质得到△MPN是等腰直角三角形,于是得到当PM最小时,对角线MN最小,即AE取最小值,当AE⊥BD时,AE取最小值,过D作DF⊥AB于F,根据平行四边形的面积得到DF=2,根据等腰直角三角形的性质得到AF=DF=2,由勾股定理得到BD=$\sqrt{D{F}^{2}+B{F}^{2}}$=$\sqrt{5}$,根据三角形的面积得到AE=$\frac{DF•AB}{BD}$=$\frac{2×3}{\sqrt{5}}$=$\frac{6\sqrt{5}}{5}$,即可得到结论.
解答 解:∵△ABE≌△CDF≌△PMQ,
∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,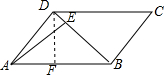
∵平行四边形ABCD的面积为6,AB=3,
∴DF=2,
∵∠DAB=45°,
∴AF=DF=2,
∴BF=1,
∴BD=$\sqrt{D{F}^{2}+B{F}^{2}}$=$\sqrt{5}$,
∴AE=$\frac{DF•AB}{BD}$=$\frac{2×3}{\sqrt{5}}$=$\frac{6\sqrt{5}}{5}$,
∴MN=$\sqrt{2}$AE=$\frac{6\sqrt{10}}{5}$,
故答案为:$\frac{6\sqrt{10}}{5}$.
点评 本题考查了平移的性质,翻折的性质,勾股定理,平行四边形的性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
11.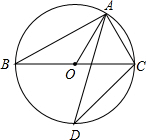 如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
 如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
12.在△ABC中,若点D为AB中点,点E是AC上一点,则下列条件能判断线段DE一定为△ABC中位线的是( )
| A. | DE⊥AC | B. | CE=2AE | ||
| C. | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=1 | D. | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=$\frac{1}{3}$ |
9.如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为( )


| A. | $\sqrt{3}$m | B. | 2$\sqrt{3}$m | C. | 4$\sqrt{3}$m | D. | 6$\sqrt{3}$m |
16. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )| A. | 12.5° | B. | 15° | C. | 20° | D. | 22.5° |
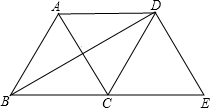 如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论: