题目内容
3. 证明:三角形中位线定理.
证明:三角形中位线定理.已知:如图,DE是△ABC的中位线.
求证:DE∥BC,DE=$\frac{1}{2}$BC.
证明:略.
分析 作出图形,然后写出已知、求证,延长DE到F,使DE=EF,利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得DE∥BC,DE=$\frac{1}{2}$BC.
解答 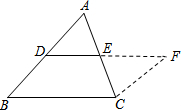 求证:DE∥BC,DE=$\frac{1}{2}$BC.
求证:DE∥BC,DE=$\frac{1}{2}$BC.
证明:如图,延长DE到F,使FE=DE,连接CF,
在△ADE和△CFE中,
$\left\{\begin{array}{l}{AE=EC}\\{∠AED=∠CEF}\\{DE=EF}\end{array}\right.$,
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=$\frac{1}{2}$BC.
点评 本题考查了三角形的中位线定理的证明,关键在于作辅助线构造成全等三角形和平行四边形,文字叙述性命题的证明思路和方法需熟练掌握.

练习册系列答案
相关题目
13.一个数的算术平方根等于它本身,则这个数应是( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 1或0 |
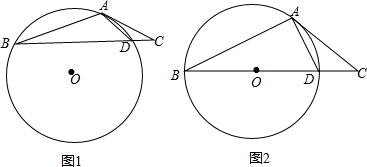
11. 如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
 如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )
如图,A、D是⊙O上的两点,BC是直径,若∠D=35°,则∠OCA的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
15. 如图是折幸运星的第一步图解,即将纸带打一个结并拉紧压平,图中AB是这个正五边形的一条边,点C是折叠后的最右边端点,则∠ABC的度数是( )
如图是折幸运星的第一步图解,即将纸带打一个结并拉紧压平,图中AB是这个正五边形的一条边,点C是折叠后的最右边端点,则∠ABC的度数是( )
 如图是折幸运星的第一步图解,即将纸带打一个结并拉紧压平,图中AB是这个正五边形的一条边,点C是折叠后的最右边端点,则∠ABC的度数是( )
如图是折幸运星的第一步图解,即将纸带打一个结并拉紧压平,图中AB是这个正五边形的一条边,点C是折叠后的最右边端点,则∠ABC的度数是( )| A. | 108° | B. | 120° | C. | 144° | D. | 135° |
12.在△ABC中,若点D为AB中点,点E是AC上一点,则下列条件能判断线段DE一定为△ABC中位线的是( )
| A. | DE⊥AC | B. | CE=2AE | ||
| C. | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=1 | D. | $\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=$\frac{1}{3}$ |
 作图题
作图题