题目内容
1.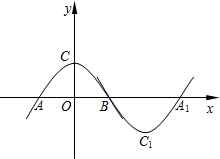 如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1
如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1(1)当a=-1,b=1时,求B点坐标及抛物线l2的解析式;
(2)若a=-$\frac{1}{2}$,且四边形AC1A1C为矩形,求抛物线l1的解析式.
分析 (1)将a,b的值代入抛物线解析式,即可求得点A,B,C,C1 的坐标,即可求得抛物线l2的解析式;
(2)易证△ABC是正三角形,即可求得a、b的关系,即可解题.
解答 解:(1)当a=-1,b=1,
则抛物线l1 解析式为:y=-x2+1,
当y=0时,x=1或-1,∴点B坐标为(1,0);点C坐标为(0,1);
∵抛物线l2是抛物线l1旋转而来,∴点C1 坐标为(2,-1),点A1 坐标为(3,0);
设抛物线l2的解析式为y=ax2+bx+c,∵抛物线l2是经过A1,C1,B点,
代入得:$\left\{\begin{array}{l}{a+b+c=0}\\{4a+2b+c=-1}\\{9a+3b+c=0}\end{array}\right.$,解得:a=1,b=-4,c=3,
∴抛物线l2的解析式y=x2-4x+3;
(2)连接AC,CC1,AC1,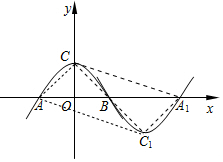
∵四边形AC1A1C为矩形,∴AB=BC,
∵抛物线l1关于y轴对称,∴AC=BC,
∴AB=BC=AC,
∴△ABC为等边三角形;
∵当y=ax2+b=0时,x=±$\sqrt{\frac{b}{a}}$,
∴点A坐标(-$\sqrt{\frac{b}{a}}$,0),点B坐标($\sqrt{\frac{b}{a}}$,0),点C坐标(0,b);
∵在Rt△AOC中,AC=$\sqrt{{AO}^{2}{+CO}^{2}}$=$\sqrt{\frac{b}{a}{+b}^{2}}$,AB=2$\sqrt{\frac{b}{a}}$,
∴$\sqrt{\frac{b}{a}{+b}^{2}}$=2$\sqrt{\frac{b}{a}}$,
解得:b=$\frac{3}{a}$=-6;
∴抛物线l1的解析式为y=-$\frac{1}{2}$x2-6.
点评 本题考查了代入法求二次函数解析式的方法,考查了对称的性质,考查了矩形对角线互相平分的性质,考查了正三角形的判定和性质.

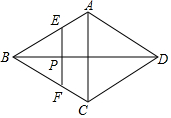 如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )
如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )| A. | 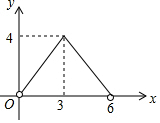 | B. | 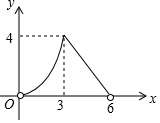 | ||
| C. | 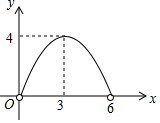 | D. | 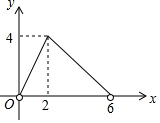 |
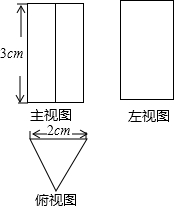 如图是一个几何体的三视图,则这个几何体的体积是( )
如图是一个几何体的三视图,则这个几何体的体积是( )| A. | 3$\sqrt{3}$cm3 | B. | 6$\sqrt{3}$cm3 | C. | 6cm3 | D. | 12cm3 |
| A. | 3 | B. | 0 | C. | π | D. | -4 |
| A. | 方差是21 | B. | 平均数是26 | C. | 众数是22 | D. | 中位数是24 |
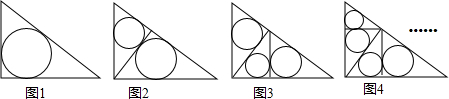
| A. | 4π | B. | 3π | C. | 2π | D. | π |
| A. | 8a2-4a=4a | B. | (-a3b)2=a6b2 | C. | a-2+a2=a0 | D. | a2•4a4=4a8 |
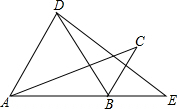 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )| A. | ∠ABD=∠E | B. | ∠CBE=∠C | C. | AD∥BC | D. | AD=BC |
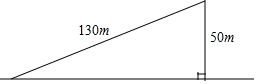 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于( )
如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{13}{12}$ |