题目内容
11.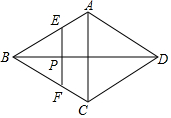 如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )
如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )| A. | 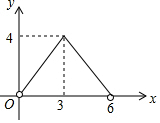 | B. | 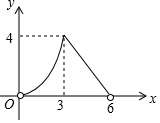 | ||
| C. | 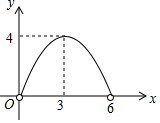 | D. | 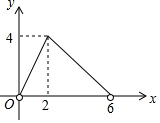 |
分析 由EF∥AC,可证△BEF∽△BAC,利用相似三角形对应边上高线的比等于相似比,得出函数关系式,判断函数图象.
解答 解:如图,
∵在菱形ABCD中,AC=4,BD=6,
∴AC⊥BD,BO=DO=3,AO=CO=2,
∵EF∥AC,
∴BD⊥EF,
当0≤x≤3时,
∵EF∥AC,
∴△BEF∽△BAC,
∴$\frac{BP}{BO}=\frac{EF}{AC}$,即$\frac{x}{3}=\frac{y}{4}$,解得y=$\frac{4}{3}$x,
同理可得,当3<x≤6时,y=$\frac{4}{3}$(6-x).
故选A.
点评 本题考查了动点问题的函数图象.关键是根据图形,利用相似三角形的性质得出分段函数关系式.

练习册系列答案
相关题目
1.一次函数y=(2a-1)x+6的图象与坐标轴在第二象限围成的三角形的面积为6,则a的值为( )
| A. | a=2 | B. | a=-2 | C. | a=1 | D. | a=-1 |
2.|-2017|的相反数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
19.分解因式:x2y-4y结果正确的是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+2)2 | D. | y(x+2)(x-2) |
6.若二次根式$\sqrt{2x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≤3 | B. | x>3 | C. | x≥3 | D. | x>-3 |
16.下列运算正确的是( )
| A. | $\frac{1}{x}-\frac{1}{y}=\frac{x-y}{xy}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | C. | $\frac{-a-1}{{{a^2}-1}}=-\frac{1}{a+1}$ | D. | $\frac{{{a^2}-1}}{a}•\frac{1}{a+1}=-1$ |
3.肥皂泡的泡壁厚度大约是0.0000007m,用科学记数法可表示为( )m.
| A. | 0.7×10-6 | B. | 0.7×10-7 | C. | 7×10-6 | D. | 7×10-7 |
20. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
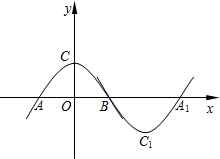 如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1
如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1