题目内容
10．
如图，在?ABCD中，DB=DC，∠C=72°，AE⊥BD于E，求∠DAE的度数．
分析 在△BCD中，利用等腰三角形的性质求得∠CBD的度数，然后利用平行线的性质求得∠ADB的度数，在直角△ADE中，利用直角三角形的性质求解．
解答 解：∵DB=DC，
∴∠CBD=∠C=72°，
又∵平行四边形ABCD中，AD∥BC，
∴∠ADB=∠CBD=72°，
∵AE⊥BD于E，
∴在直角△ADE中，∠DAE=90°-∠ADB=90°-72°=18°．
点评 本题考查了等腰三角形的性质：等边对等角以及平行线的性质和直角三角形的性质，直角三角形的两锐角互余．
练习册系列答案
天天向上口算本系列答案
相关题目
20．
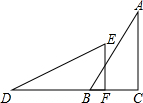如图，△ABC≌△DEF，∠C=∠DFE=90°，A与D是 对应点，要使△DEF通过几何变换与△ABC重合，必须有的变换是（ ）
如图，△ABC≌△DEF，∠C=∠DFE=90°，A与D是 对应点，要使△DEF通过几何变换与△ABC重合，必须有的变换是（ ）| A． | 轴对称 | B． | 平移 | C． | 旋转 | D． | 中心对称 |
15．
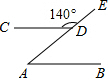如图，AB∥CD，∠CDE=140°，则∠A的度数为（ ）
如图，AB∥CD，∠CDE=140°，则∠A的度数为（ ）| A． | 70° | B． | 65° | C． | 50° | D． | 40° |
王霞和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴、y轴．只知道游乐园D的坐标为（1，-2），你能帮她求出其他各景点的坐标吗？
如图，E（2，3），F（3，2）在正方形OABC的边上，⊙D分别切OE，OF于E，F，则⊙D的半径为$\frac{{\sqrt{13}}}{5}$．