题目内容
6. 如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.
如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 作OE⊥AB交AB于E,由OB平分∠ABC,OH⊥BC,得到OE=OH=3cm,根据角平分线的定义得到∠BAO=30°,根据直角三角形的性质即可得到结论.
解答  解:作OE⊥AB交AB于E,
解:作OE⊥AB交AB于E,
∵OB平分∠ABC,OH⊥BC,
∴OE=OH=3cm,
∵∠ABC,∠ACB的角平分线交于点O,
∴AO平分∠BAC,
∵∠BAC=60°,
∴∠BAO=30°,
∴AO=2OE=6cm,
故选A.
点评 本题考查了角平分线的性质,直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
18.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6$\sqrt{2}$,则AC长是( )
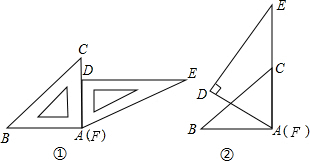

| A. | 6+2$\sqrt{3}$ | B. | 9 | C. | 10 | D. | 6+6$\sqrt{2}$ |
16. 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
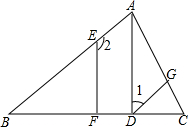 如图:已知AD⊥BC于点D,∠1+∠2=180°,∠B=∠CDG,试判断EF与BC的位置关系并说明理由.
如图:已知AD⊥BC于点D,∠1+∠2=180°,∠B=∠CDG,试判断EF与BC的位置关系并说明理由.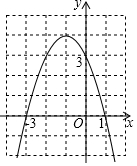 二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )
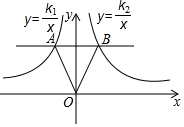 如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12.
如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12.