题目内容
14.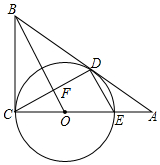 如图,Rt△ABC中,∠ACB=90°,点O是AC上一点,以OC为半径作⊙O与AB相切于D,交AC于点E,OB交CD于F.
如图,Rt△ABC中,∠ACB=90°,点O是AC上一点,以OC为半径作⊙O与AB相切于D,交AC于点E,OB交CD于F.(1)证明:OB•DE=$\frac{1}{2}$CE2;
(2)若$\frac{OF}{OB}$=$\frac{1}{5}$,AB=10,求⊙O的半径.
分析 (1)先证明△COF∽△BOC,可得OC2=OF•OB,再根据CE=2OC,DE=2OF,即可解决问题;
(2)由OF:OB=1:5,设OF=a,OB=5a,则DE=2a.由DE∥OB,推出$\frac{AD}{AB}$=$\frac{DE}{OB}$=$\frac{2}{5}$,推出AD=4,BD=6,根据$\frac{1}{2}$CE2=DE•OB=10a2,推出CE=2$\sqrt{5}$a,推出OD=$\sqrt{5}$a,在Rt△BDO中,根据BD2+OD2=OB2,列出方程求出a即可解决问题;
解答 (1)证明:∵∠ACB=90°,
∴OC⊥BC,
∴BC是⊙O的切线,∵AB是⊙O的切线,
∴BC=BD,∵OD=OC,
∴OB垂直平分CD,
∴CF=DF,∵OC=OE,
∴DE=2OF,
∵∠COF=∠BOC,∠CFO=∠OCB=90°,
∴△COF∽△BOC,
∴OC2=OF•OB,
∴4OC2=4OF•OB=2DE•OB,
∴CE2=2DE•OB,
∴$\frac{1}{2}$CE2=DE•OB.
(2)∵OF:OB=1:5,设OF=a,OB=5a,则DE=2a.
∵CE是直径,
∴∠CDE=90°,
∴∠CFO=∠CDE=90°,
∴DE∥OB,
∴$\frac{AD}{AB}$=$\frac{DE}{OB}$=$\frac{2}{5}$,
∴AD=4,BD=6,
∵$\frac{1}{2}$CE2=DE•OB=10a2,
∴CE=2$\sqrt{5}$a,
∴OD=$\sqrt{5}$a,
在Rt△BDO中,BD2+OD2=OB2,
∴36+5a2=25a2,
∴a2=$\frac{9}{5}$,
∵a>0,
∴a=$\frac{3\sqrt{5}}{5}$,
∴OD=3,
∴⊙O的半径为3.
点评 本题考查相似三角形的判定和性质、切线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )| A. | ①②③ | B. | ①④⑤ | C. | ③④⑤ | D. | ①③⑤ |
| A. | 7 | B. | 5 | C. | 7或3 | D. | 3 |
| A. | 20个 | B. | 28个 | C. | 36个 | D. | 32个 |
| A. | -1 | B. | 1 | C. | 0.25 | D. | 45000 |