题目内容
5. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )| A. | ①②③ | B. | ①④⑤ | C. | ③④⑤ | D. | ①③⑤ |
分析 由抛物线的位置以及对称轴易判断a,b,c的符号以及判别式的符号,再由对称性可求得抛物线与x轴的另一交点坐标为(-1,0),容易判断④,根据抛物线的增减性即可判断⑤.
解答 解:
∵二次函数y=ax2+bx+c过点A (3,0),对称轴是x=1,
∴抛物线与x轴的另一交点坐标为(-1,0),
∴当x=-1时,y=0,即a-b+c=0,故③错误;
∵开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∴ac<0,故②错误;
∵抛物线与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,即b2>4ac,故①正确;
∵二次函数y=ax2+bx+c的图象过点A(3,0),对称轴是x=1,
∴二次函数y=ax2+bx+c与x轴的交点坐标是(-1,0),(3,0),
结合图象可知当-1<x<3,ax2+bx+c>0,
∴不等式ax2+bx+c>0的解集是-1<x<3,故选项④正确;
由图象和二次函数图象的对称轴是x=1,可得当x>1时,y随x的增大而减小,故选项⑤正确,
故选B.
点评 此题主要考查二次函数图象与系数的关系,掌握a、b、c与二次函数的图象的关系是解题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
16.A、B两种型号的机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用时间与B型机器人搬运600千克所用时间相等.设B型机器人每小时搬运x千克,则x满足的方程是( )
| A. | $\frac{900}{x}$=$\frac{600}{x+30}$ | B. | $\frac{900}{x}$=$\frac{600}{x-30}$ | C. | $\frac{600}{x}$=$\frac{900}{x+30}$ | D. | $\frac{600}{x}$=$\frac{900}{x-30}$ |
 已知在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为(3,-1).
已知在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为(3,-1).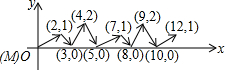 如图,动点M在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,1),第2次运动到点(3,0),第3次运动到点(4,2),…,按这样的运动规律,经过第2017次运动后,动点M的坐标是(2522,1).
如图,动点M在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,1),第2次运动到点(3,0),第3次运动到点(4,2),…,按这样的运动规律,经过第2017次运动后,动点M的坐标是(2522,1).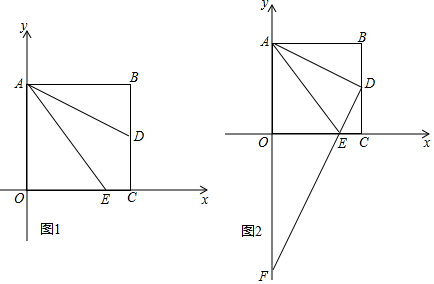
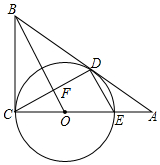 如图,Rt△ABC中,∠ACB=90°,点O是AC上一点,以OC为半径作⊙O与AB相切于D,交AC于点E,OB交CD于F.
如图,Rt△ABC中,∠ACB=90°,点O是AC上一点,以OC为半径作⊙O与AB相切于D,交AC于点E,OB交CD于F.