题目内容
13.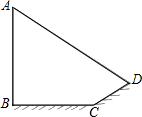 已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.
已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.
分析 延长AD交BC的延长线于点E,作DF⊥BE于F,构造含30°的2个直角三角形,利用45°的三角函数值可得DF和CF的长,进而利用30°的正切值可求得EF长,再求得BE长,然后利用30°的正切值求得AB长即可.
解答  解:如图,延长AD交BC的延长线于点E,作DF⊥BE于F.
解:如图,延长AD交BC的延长线于点E,作DF⊥BE于F.
∵在Rt△DCF中,∠CFD=90°,∠DCF=45°,CD=4$\sqrt{2}$,
∴CF=DF=4.
∵在Rt△DEF中,∠EFD=90°,∠E=30°,
∴EF=$\frac{DF}{tan∠E}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$,
∴BE=BC+CF+FE=4$\sqrt{3}$-4+4+4$\sqrt{3}$=8$\sqrt{3}$.
∵在Rt△ABE中,∠B=90°,∠E=30°,
∴AB=BEtan30°=8$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=8.
故电线杆AB的长为8米.
点评 此题考查了解直角三角形的应用,锐角三角函数的定义.准确作出辅助线进而求出BE=BC+CF+FE是解题的关键.

练习册系列答案
相关题目
3.若一组数据1,2,3,7,x的平均数是3,则这组数的众数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 7 |
8.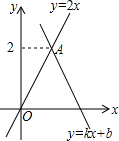 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
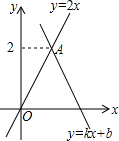 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | x>0 | B. | 0<x<1 | C. | 1<x<2 | D. | x>2 |
18.下列四个数中,最大的数是( )
| A. | 2 | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
2.已知x1、x2是方程x2-5x-6=0的两个根,则代数式x1•x2-x1-x2的值是( )
| A. | 11 | B. | -1 | C. | -11 | D. | 1 |
 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.