题目内容
3. 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°.求图中所示阴影部分的面积.
分析 (1)连结OC,如图,由∠1=∠2,∠2=∠3得∠1=∠3,则可判断OC∥AD,由于CD⊥AD,所以OC⊥CD,于是根据切线的判定定理可得CD为⊙O的切线;
(2)利用三角形外角性质可得到∠EOC=60°,而OC⊥CD,则∠OCE=90°,在Rt△OCE中利用∠EOC的正切可计算出CE=3$\sqrt{3}$,然后三角形面积公式和扇形面积公式,利用S阴影部分=S△OOE-S扇形COB进行计算即可.
解答  解:(1)CD与⊙O相切.理由如下:
解:(1)CD与⊙O相切.理由如下:
连结OC,如图,
∵OA=OC,
∴∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
而CD⊥AD,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵∠EOC=∠1+∠2,∠2=30°,
∴∠EOC=60°,
∵OC⊥CD,
∴∠OCE=90°,
在Rt△OCE中,∵tan∠EOC=$\frac{CE}{OC}$,
∴CE=3tan60°=3$\sqrt{3}$,
∴S阴影部分=S△OOE-S扇形COB
=$\frac{1}{2}$×3×3$\sqrt{3}$-$\frac{60•π•{3}^{2}}{360}$
=$\frac{9\sqrt{3}-3π}{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积的计算.

练习册系列答案
相关题目
14.已知二次函数y=ax2+bx+c中的x,y满足下表:
根据表中信息,下列判断不正确的是( )
| X | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | … |
| A. | 开口向上 | B. | 当-1<x<2时,y<0 | ||
| C. | 图象的对称轴是直线x=$\frac{1}{2}$ | D. | 函数最小值是-2 |
8.下列说法中正确的是( )
| A. | 篮球队员在罚球线上投篮一次,未投中是必然事件 | |
| B. | 想了解某种饮料中含色素的情况,宜采用普查 | |
| C. | 数据5,1,-2,2,3的中位数是-2 | |
| D. | 一组数据的波动越大,方差越大 |
13. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
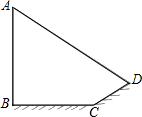 已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.
已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.