题目内容
19.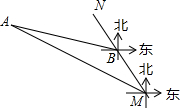 如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)
如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)
分析 问输水线路是否会穿过居民区,其实就是求A到MN的距离是否大于圆形居民区的半径,如果大于则不会穿过,反之则会.
解答  解:过A作AD⊥MN于点D
解:过A作AD⊥MN于点D
设AD=x,
∵∠ABD=45°,
∴设BD=x,
∵∠AMD=30°,
∴$tan∠AMD=\frac{AD}{MD}$$\frac{{\sqrt{3}}}{3}-\frac{x}{x+400}$,
x=546.372AD>500.
∴不会穿过居民区.
点评 本题考查了解直角三角形,当两个直角三角形有公共的直角边时,利用这条公共边来求解是解决此类题目的基本出发点.

练习册系列答案
相关题目
10.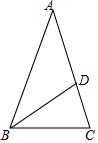 如图,△ABC中,AB=AC,∠A=30°,以B为圆心,以BC为半径画弧交AC于点D,那么∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=30°,以B为圆心,以BC为半径画弧交AC于点D,那么∠DBC的度数是( )
 如图,△ABC中,AB=AC,∠A=30°,以B为圆心,以BC为半径画弧交AC于点D,那么∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=30°,以B为圆心,以BC为半径画弧交AC于点D,那么∠DBC的度数是( )| A. | 30° | B. | 45° | C. | 40° | D. | 60° |
7.点A为数轴上表示-1的点,将点A在数轴上平移3个单位长度到点B,则点B所表示的实数为( )
| A. | 3 | B. | 2 | C. | -4 | D. | 2或-4 |
11.山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
| A. | 140元 | B. | 150元 | C. | 160元 | D. | 180元 |
8.用反证法证明命题:“△ABC中,若AB=AC,则∠B、∠C都是锐角”首先应假设( )
| A. | ∠B、∠C都不是锐角 | B. | ∠B为锐角 | C. | ∠C不为锐角 | D. | ∠B、∠C不都是锐角 |
 如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.
如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.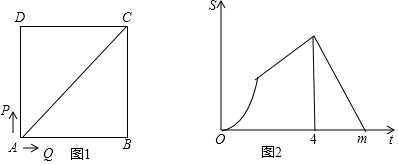
 将一块直角三角板与一两边平行的纸条按如图所示位置放置,若∠1=20°,则∠2=70°.
将一块直角三角板与一两边平行的纸条按如图所示位置放置,若∠1=20°,则∠2=70°.