题目内容
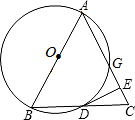 如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.
如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.(1)试确定直线DE与⊙O的位置关系,并说明理由;
(2)若CD=2,AC=5,求CG的长.
考点:切线的判定,等腰三角形的性质,解直角三角形
专题:
分析:(1)连接OD,AD,根据圆周角定理由AB为直径得∠ADB=90°,而AB=AC,根据等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,根据平行线的性质有OD⊥DE,然后根据切线的判定定理得到DE与⊙O相切;
(2)连结BG,根据圆周角定理由AB是⊙O的直径得∠AGB=90°,由CD=2得BC=2CD=4,然后证明Rt△ADC∽Rt△BCG,利用相似比可计算出CG.
(2)连结BG,根据圆周角定理由AB是⊙O的直径得∠AGB=90°,由CD=2得BC=2CD=4,然后证明Rt△ADC∽Rt△BCG,利用相似比可计算出CG.
解答: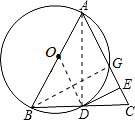 解:(1)直线DE与⊙O相切.理由如下:
解:(1)直线DE与⊙O相切.理由如下:
连接OD,AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE与⊙O相切;
(2)连结BG,如图,
∵AB是⊙O的直径,
∴∠AGB=90°,
∵CD=2,
∴BC=2CD=4,
∵∠ACD=∠BCG,
∴Rt△ADC∽Rt△BCG,
∴
=
,即
=
∴CG=
.
 解:(1)直线DE与⊙O相切.理由如下:
解:(1)直线DE与⊙O相切.理由如下:连接OD,AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE与⊙O相切;
(2)连结BG,如图,
∵AB是⊙O的直径,
∴∠AGB=90°,
∵CD=2,
∴BC=2CD=4,
∵∠ACD=∠BCG,
∴Rt△ADC∽Rt△BCG,
∴
| CD |
| CG |
| AC |
| BC |
| 2 |
| CG |
| 5 |
| 4 |
∴CG=
| 8 |
| 5 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
当实数x的取值,使得
有意义时,函数y=-2x+1中,y的取值范围是( )
| x-2 |
| A、y≤-3 | B、y≥-3 |
| C、y≤5 | D、y≥5 |
 如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.
如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.