题目内容
(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)已知13x2-6xy+y2-4x+1=0,求:(x+y)2013•x2012的值.
(2)已知13x2-6xy+y2-4x+1=0,求:(x+y)2013•x2012的值.
考点:完全平方公式,因式分解的应用
专题:
分析:(1)灵活运用(a+b)2与(a-b)2,化出a2+b2和ab的式子求值.
(2)把13x2-6xy+y2-4x+1=0化为(3x-y)2+(2x-1)2=0,求出x,y的值再求出结果.
(2)把13x2-6xy+y2-4x+1=0化为(3x-y)2+(2x-1)2=0,求出x,y的值再求出结果.
解答:解:(1)∵(a+b)2=7,(a-b)2=4,
∴a2+b2=[(a+b)2+(a-b)2]÷2=(7+4)÷2=
ab=[(a+b)2-(a-b)2]÷4=
.
(2)∵13x2-6xy+y2-4x+1=0,
∴(3x-y)2+(2x-1)2=0,
解得,x=
,y=
,
∴(x+y)2013•x2012=(
+
)2013(
)2012=(2×
)2012×2=2.
∴a2+b2=[(a+b)2+(a-b)2]÷2=(7+4)÷2=
| 11 |
| 2 |
ab=[(a+b)2-(a-b)2]÷4=
| 3 |
| 4 |
(2)∵13x2-6xy+y2-4x+1=0,
∴(3x-y)2+(2x-1)2=0,
解得,x=
| 1 |
| 2 |
| 3 |
| 2 |
∴(x+y)2013•x2012=(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了完全平方公式与因式分解的应用,解题的关键是转式子简求出x,y的值.

练习册系列答案
相关题目
一个长方形的周长是26cm,若这个长方形的长减少1cm,宽增加2cm,就可以成为一个正方形,则此正方形的边长是( )
| A、5cm | B、6cm |
| C、7cm | D、8cm |
关于x,y的方程组
的解是
,则|m+n|的值是( )
|
|
| A、9 | B、5 | C、4 | D、1 |
 如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= 推理填空:
推理填空: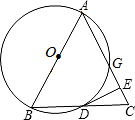 如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.
如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.