题目内容
 如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.
如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.(1)画出三角形A1B1C1,并分别写出三个顶点的坐标;
(2)求出平移后的三角形A1B1C1的面积.
考点:作图-平移变换
专题:作图题
分析:(1)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(2)利用△A1B1C1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
(2)利用△A1B1C1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
解答: 解:(1)△A1B1C1如图所示,A1(3,-2),B1(0,-3),C1(1,-4);
解:(1)△A1B1C1如图所示,A1(3,-2),B1(0,-3),C1(1,-4);
(2)△A1B1C1的面积=3×2-
×1×1-
×2×2-
×1×3
=6-0.5-2-1.5
=6-4
=2.
 解:(1)△A1B1C1如图所示,A1(3,-2),B1(0,-3),C1(1,-4);
解:(1)△A1B1C1如图所示,A1(3,-2),B1(0,-3),C1(1,-4);(2)△A1B1C1的面积=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-0.5-2-1.5
=6-4
=2.
点评:本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
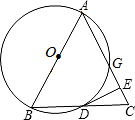 如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.
如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AC于点 G,过D点作DE上AC于点E.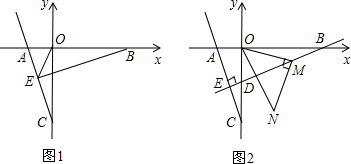
 不等式组里每个不等式的解集表示在同一数轴上如图,则此不等式组的解集用x表示为
不等式组里每个不等式的解集表示在同一数轴上如图,则此不等式组的解集用x表示为