ΧβΡΩΡΎ»ί
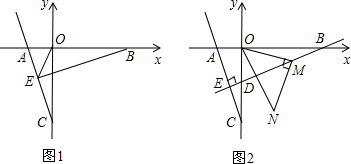
»γΆΦΘ§Β»―ϋΧί–ΈABCDΒΡΒΉ±ΏAB‘Ύx÷α…œΘ§«“ΒψA”κ‘≠ΒψO÷ΊΚœΘ§ΒψBΉχ±ξΈΣΘ®8
Θ§0Θ©Θ§ΒψDΉχ±ξΈΣΘ®3
Θ§3
Θ©Θ§ΒψEΈΣAB±Ώ…œ“ΜΕ·ΒψΘ§“‘ΟΩΟκ
ΗωΒΞΈΜΒΡΥΌΕ»”…AœρB‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΘ§ΫΪ…δœΏED»ΤEΒψΥ≥ ±’κ–ΐΉΣ45ΓψΫΜBC”ΎFΒψΘ°
Θ®1Θ©«σΨ≠ΙΐAΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΘΜ
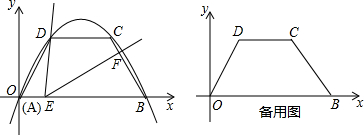
Θ®2Θ©«σ≥ωœΏΕΈBFΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»τΓςADEΈΣΒ»―ϋ»ΐΫ«–ΈΘ§«σt÷ΒΘΜ
Θ®4Θ©‘Ύ÷±œΏBC…œ»Γ“ΜΒψPΘ§«σDE+EPΒΡΉν–Γ÷ΒΘ°
| 2 |
| 2 |
| 2 |
| 2 |

Θ®1Θ©«σΨ≠ΙΐAΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΘΜ
Θ®2Θ©«σ≥ωœΏΕΈBFΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»τΓςADEΈΣΒ»―ϋ»ΐΫ«–ΈΘ§«σt÷ΒΘΜ
Θ®4Θ©‘Ύ÷±œΏBC…œ»Γ“ΜΒψPΘ§«σDE+EPΒΡΉν–Γ÷ΒΘ°
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©ΙΐDΉςDDΓδΓΆAB”ΎDΓδΘ§ΙΐCΉςCCΓδΓΆAB”ΎCΓδΘ§Ω…ΒΟCΒψΉχ±ξΈΣΘ®5
Θ§0Θ©Θ§‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σΒΟΙΐAΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΘΜ
Θ®2Θ©ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®Ω…ΒΟΓςADEΓΉΓςBEFΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ
=
Θ§…ηBF=yΘ§Ω…ΒΟy=-
(t-4)2+
Θ§¥”ΕχΒΟΒΫœΏΕΈBFΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©Ζ÷»ΐ÷÷«ιΩωΘΚΔΌΒ±ED=EA ±Θ®»γΒψE1Θ©ΘΜΔΎΒ±AD=AE ±Θ®»γΒψE2Θ©ΘΜΔέΒ±DA=DE ±Θ®»γΒψE3Θ©ΘΜΧ÷¬έΩ…ΒΟΓςADE «Β»―ϋ»ΐΫ«–Έ ±tΒΡ÷ΒΘΜ
Θ®4Θ©ΉςΒψDΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψDΓδΘ§ΙΐDΓδΉςDΓδPΓΆCB”ΎPΘ§Ν§Ϋ”DΓδPΫΜOB”ΎΒψEΘ§”…÷αΕ‘≥Τ÷ΣDE+EP=DΓδE+EP=DΓδPΘ§”…¥ΙœΏΕΈΉνΕΧ÷Σ¥Υ ±DΓδPΉνΕΧΘ§‘ρDE+EP“≤Ήν–ΓΘ°
| 2 |
Θ®2Θ©ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®Ω…ΒΟΓςADEΓΉΓςBEFΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ
| AD |
| BE |
| AE |
| BF |
| 1 |
| 3 |
| 16 |
| 3 |
Θ®3Θ©Ζ÷»ΐ÷÷«ιΩωΘΚΔΌΒ±ED=EA ±Θ®»γΒψE1Θ©ΘΜΔΎΒ±AD=AE ±Θ®»γΒψE2Θ©ΘΜΔέΒ±DA=DE ±Θ®»γΒψE3Θ©ΘΜΧ÷¬έΩ…ΒΟΓςADE «Β»―ϋ»ΐΫ«–Έ ±tΒΡ÷ΒΘΜ
Θ®4Θ©ΉςΒψDΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψDΓδΘ§ΙΐDΓδΉςDΓδPΓΆCB”ΎPΘ§Ν§Ϋ”DΓδPΫΜOB”ΎΒψEΘ§”…÷αΕ‘≥Τ÷ΣDE+EP=DΓδE+EP=DΓδPΘ§”…¥ΙœΏΕΈΉνΕΧ÷Σ¥Υ ±DΓδPΉνΕΧΘ§‘ρDE+EP“≤Ήν–ΓΘ°
Ϋβ¥πΘΚ ΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΙΐDΉςDDΓδΓΆAB”ΎDΓδΘ§ΙΐCΉςCCΓδΓΆAB”ΎCΓδΘ§
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΙΐDΉςDDΓδΓΆAB”ΎDΓδΘ§ΙΐCΉςCCΓδΓΆAB”ΎCΓδΘ§
Ω…«σΒΟBCΓδ=ODΓδ=3
Θ§CCΓδ=DDΓδ=3
Θ§DΓδCΓδ=DC=2
Θ§
‘ρCΒψΉχ±ξΈΣΘ®5
Θ§0Θ©Θ§
‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σΒΟΙΐAΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΈΣy=-
x2+
x
Θ®2Θ©»γΆΦ2Θ§ΦΤΥψ÷ΣΓœCBA=ΓœDAB=ΓœDEF=45ΓψΘ§Γœ1+Γœ2=135ΓψΘ§Γœ2+Γœ3=135ΓψΘ§
Υυ“‘Γœ1=Γœ3Θ§ΓςADEΓΉΓςBEFΘ§
‘ρ
=
Θ§
…ηBF=yΘ§Φ¥”–
=
Θ§
Μ·ΦρΒΟΘΚy=-
t2+
tȧ
≈δΖΫΒΟy=-
(t-4)2+
Θ§
Β±t=4 ±Θ§y”–Ήν¥σ÷Β«“ΈΣ
Θ§Φ¥BFΉν¥σΈΣ
 Θ®3Θ©»γΆΦ3”……œΆΦΦΤΥψ÷ΣAD=
Θ®3Θ©»γΆΦ3”……œΆΦΦΤΥψ÷ΣAD=
ADΓδ=6Θ§ΓœBAD=45ΓψΘΜ
ΔΌΒ±ED=EA ±Θ®»γΒψE1Θ©Θ§‘ρΓœE1AD=ΓœE1DA=45ΓψΘ§DE1ΓΆABΘ§‘ρE1”κ…œΆΦ÷–ΒΡDΓδ÷ΊΚœΘ§Ι OE1=3
Θ§t=3
Γ¬
=3ΘΜ
ΔΎΒ±AD=AE ±Θ®»γΒψE2Θ©Θ§‘ρAE2=AD=6Θ§t=6Γ¬
=3
ΘΜ
ΔέΒ±DA=DE ±Θ®»γΒψE3Θ©Θ§”…ΓΑ»ΐœΏΚœ“ΜΓ±ΒΟAE3=2AE1=6
Γ¬
=6
Ήέ…œΥυ ωΘ§Β±t=3Θ§3
Θ§6 ±Θ§ΓςADE «Β»―ϋ»ΐΫ«–ΈΘ°
Θ®4Θ©»γΆΦ4Θ§ΉςΒψDΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψDΓδΘ§ΙΐDΓδΉςDΓδPΓΆCB”ΎPΘ§Ν§Ϋ”DΓδPΫΜOB”ΎΒψEΘ§
”…÷αΕ‘≥Τ÷ΣDE+EP=DΓδE+EP=DΓδPΘ§
”…¥ΙœΏΕΈΉνΕΧ÷Σ¥Υ ±DΓδPΉνΕΧΘ§‘ρDE+EP“≤Ήν–ΓΘ°
”…ΓœCBO=45ΓψΘ§Ω…ΆΤΒΦDΓδE=
DΓδF=
DF=
•3
=6Θ§BE=BF-FG=2
Θ§EP=
=2Θ§
Υυ“‘DΓδP=8Θ§Φ¥DE+EPΉν–Γ÷ΒΈΣ8Θ°
 ΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΙΐDΉςDDΓδΓΆAB”ΎDΓδΘ§ΙΐCΉςCCΓδΓΆAB”ΎCΓδΘ§
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΙΐDΉςDDΓδΓΆAB”ΎDΓδΘ§ΙΐCΉςCCΓδΓΆAB”ΎCΓδΘ§Ω…«σΒΟBCΓδ=ODΓδ=3
| 2 |
| 2 |
| 2 |
‘ρCΒψΉχ±ξΈΣΘ®5
| 2 |
‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σΒΟΙΐAΓΔCΓΔD»ΐΒψΒΡ≈ΉΈοœΏΈΣy=-
| ||
| 10 |
| 8 |
| 5 |
Θ®2Θ©»γΆΦ2Θ§ΦΤΥψ÷ΣΓœCBA=ΓœDAB=ΓœDEF=45ΓψΘ§Γœ1+Γœ2=135ΓψΘ§Γœ2+Γœ3=135ΓψΘ§
Υυ“‘Γœ1=Γœ3Θ§ΓςADEΓΉΓςBEFΘ§
‘ρ
| AD |
| BE |
| AE |
| BF |
…ηBF=yΘ§Φ¥”–
| 6 | ||||
8
|
| ||
| y |
Μ·ΦρΒΟΘΚy=-
| 1 |
| 3 |
| 8 |
| 3 |
≈δΖΫΒΟy=-
| 1 |
| 3 |
| 16 |
| 3 |
Β±t=4 ±Θ§y”–Ήν¥σ÷Β«“ΈΣ
| 16 |
| 3 |
| 16 |
| 3 |
 Θ®3Θ©»γΆΦ3”……œΆΦΦΤΥψ÷ΣAD=
Θ®3Θ©»γΆΦ3”……œΆΦΦΤΥψ÷ΣAD=| 2 |
ΔΌΒ±ED=EA ±Θ®»γΒψE1Θ©Θ§‘ρΓœE1AD=ΓœE1DA=45ΓψΘ§DE1ΓΆABΘ§‘ρE1”κ…œΆΦ÷–ΒΡDΓδ÷ΊΚœΘ§Ι OE1=3
| 2 |
| 2 |
| 2 |
ΔΎΒ±AD=AE ±Θ®»γΒψE2Θ©Θ§‘ρAE2=AD=6Θ§t=6Γ¬
| 2 |
| 2 |
ΔέΒ±DA=DE ±Θ®»γΒψE3Θ©Θ§”…ΓΑ»ΐœΏΚœ“ΜΓ±ΒΟAE3=2AE1=6
| 2 |
| 2 |
Ήέ…œΥυ ωΘ§Β±t=3Θ§3
| 2 |
Θ®4Θ©»γΆΦ4Θ§ΉςΒψDΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψDΓδΘ§ΙΐDΓδΉςDΓδPΓΆCB”ΎPΘ§Ν§Ϋ”DΓδPΫΜOB”ΎΒψEΘ§
”…÷αΕ‘≥Τ÷ΣDE+EP=DΓδE+EP=DΓδPΘ§
”…¥ΙœΏΕΈΉνΕΧ÷Σ¥Υ ±DΓδPΉνΕΧΘ§‘ρDE+EP“≤Ήν–ΓΘ°
”…ΓœCBO=45ΓψΘ§Ω…ΆΤΒΦDΓδE=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| BE | ||
|
Υυ“‘DΓδP=8Θ§Φ¥DE+EPΉν–Γ÷ΒΈΣ8Θ°
ΒψΤάΘΚΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§…φΦΑΒΡ÷Σ ΕΒψ”–ΘΚ¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ§œύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΚΆ–‘÷ Θ§Ήν÷ΒΈ ΧβΘ§Β»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ζ÷άύΥΦœκΘ§”…÷αΕ‘≥ΤΒΡ–‘÷ Θ§¥ΙœΏΕΈΉνΕΧΘ§ΉέΚœ–‘Ϋœ«ΩΘ§”–“ΜΕ®ΒΡΡ―Ε»Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
ΙΊ”ΎxΘ§yΒΡΖΫ≥ΧΉι
ΒΡΫβ «
Θ§‘ρ|m+n|ΒΡ÷Β «Θ®ΓΓΓΓΘ©
|
|
| AΓΔ9 | BΓΔ5 | CΓΔ4 | DΓΔ1 |
 ΆΤάμΧνΩ’ΘΚ
ΆΤάμΧνΩ’ΘΚ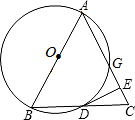 »γΆΦΘ§“‘Β»―ϋ»ΐΫ«–ΈABCΒΡ―ϋABΈΣ÷±ΨΕΒΡΓ―OΫΜΒΉ±ΏBC”ΎΒψDΘ§ΫΜ―ϋAC”ΎΒψ GΘ§ΙΐDΒψΉςDE…œAC”ΎΒψEΘ°
»γΆΦΘ§“‘Β»―ϋ»ΐΫ«–ΈABCΒΡ―ϋABΈΣ÷±ΨΕΒΡΓ―OΫΜΒΉ±ΏBC”ΎΒψDΘ§ΫΜ―ϋAC”ΎΒψ GΘ§ΙΐDΒψΉςDE…œAC”ΎΒψEΘ°