题目内容
一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时10分钟时也经过C地,未停留继续开往A地.(友情提醒:可以画出线段图帮助分析)
(1)乙车的速度是 千米/小时,B、C两地的距离是 千米,A、C两地的距离是 千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
(1)乙车的速度是
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
考点:一元一次方程的应用
专题:
分析:(1)由题意可知,甲车2小时到达C地,休息了20分钟,乙车行驶2小时10分钟也到C地,这10分钟甲车未动,即乙车10分钟走了20千米,据此可求出乙车的速度,再根据速度求出B、C两地的距离和A、C两地的距离即可解答.
(2)根据A、C两地的距离和甲车到达配货站C地的时间可求出甲车的速度,再根据行程问题的关系式求出甲车到达B地所用的时间即可解答.注意要加上配货停留的1小时.
(3)此题分为两种情况,未相遇和相遇以后相距200千米,据此根据题意列出符合题意得方程即可解答.
(2)根据A、C两地的距离和甲车到达配货站C地的时间可求出甲车的速度,再根据行程问题的关系式求出甲车到达B地所用的时间即可解答.注意要加上配货停留的1小时.
(3)此题分为两种情况,未相遇和相遇以后相距200千米,据此根据题意列出符合题意得方程即可解答.
解答:解:(1)10分钟=
小时,
乙车的速度=20÷
=120(千米/时);
B、C两地的距离=120×
=260(千米);
A、C两地的距离=380-260=120(千米);
故答案为80,180,200.
(2)甲车的速度=120÷2=60(千米/小时);
(3)设乙车出发y小时,两车相距200千米.
由题意得,120y+60y+200=380或60(y-
)+120y-200=380,
解得:x=1或x=
,
即乙车出发1小时或
小时,两车相距200千米.
| 1 |
| 6 |
乙车的速度=20÷
| 1 |
| 6 |
B、C两地的距离=120×
| 13 |
| 6 |
A、C两地的距离=380-260=120(千米);
故答案为80,180,200.
(2)甲车的速度=120÷2=60(千米/小时);
(3)设乙车出发y小时,两车相距200千米.
由题意得,120y+60y+200=380或60(y-
| 1 |
| 3 |
解得:x=1或x=
| 10 |
| 3 |
即乙车出发1小时或
| 10 |
| 3 |
点评:本题主要考查一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
下列各式:
,
,
,
(x2+1),
中,不是分式的共有( )
| a-b |
| 2 |
| x+3 |
| x |
| 5+y |
| π |
| ||
| 4 |
| a2-b2 |
| a+b |
| A、1个 | B、2个 | C、3个 | D、4个 |
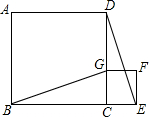 如图,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
如图,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.