题目内容
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
考点:二次函数的应用,待定系数法求一次函数解析式
专题:
分析:1)利用待定系数法求一次函数解析式即可得出答案;
(2)①首先假设一张薄板的利润为W元,它的成本价为ax2元,由题意,得:W=y-ax2,进而得出m的值,求出函数解析式即可;
②利用二次函数的最值公式求出二次函数的最值即可.
(2)①首先假设一张薄板的利润为W元,它的成本价为ax2元,由题意,得:W=y-ax2,进而得出m的值,求出函数解析式即可;
②利用二次函数的最值公式求出二次函数的最值即可.
解答:解:(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0),
由表格中的数据可得,
,
解得
,
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100;
(2)①设每张画板的成本价为ax2,利润W=6x+100-ax2,
当x=30时,W=130,180+100-900a=130,得a=
,
一张画板的利润W 与边长x之间满足函数关系式W=-
x2+6x+100;
②由W=-
(x-18)2+154,知当x=18时,W有最大值,W最大=154,
因此当正方形画板的边长为18dm时,可获最大利润154元.
由表格中的数据可得,
|
解得
|
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100;
(2)①设每张画板的成本价为ax2,利润W=6x+100-ax2,
当x=30时,W=130,180+100-900a=130,得a=
| 1 |
| 6 |
一张画板的利润W 与边长x之间满足函数关系式W=-
| 1 |
| 6 |
②由W=-
| 1 |
| 6 |
因此当正方形画板的边长为18dm时,可获最大利润154元.
点评:本题考查了二次函数的最值求法以及待定系数法求一次函数解析式,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
相关题目
下列说法正确的是( )
| A、顶点在圆上的角叫圆周角 |
| B、三点确定一个圆 |
| C、等弧所对的圆心角相等 |
| D、平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
 如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由. 操作题
操作题 如图,在一旗杆AB的顶端A上系一活动旗帜,在某一时刻,旗杆的影子落在平地BD和一坡度为1:
如图,在一旗杆AB的顶端A上系一活动旗帜,在某一时刻,旗杆的影子落在平地BD和一坡度为1: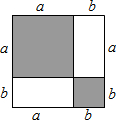 我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题: