题目内容
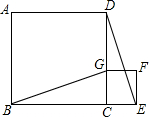 如图,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
如图,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.(1)求证:BG=DE;
(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
考点:旋转的性质,正方形的性质
专题:
分析:(1)根据正方形的性质和全等三角形的判定方法可证明△BCG≌△DCE,由全等三角形的性质即可得到BG=DE;
(2)存在,△BCG和△DCE可以通过旋转重合.求证△BCG≌△DCE即可.
(2)存在,△BCG和△DCE可以通过旋转重合.求证△BCG≌△DCE即可.
解答:(1)证明:∵四边形ABCD与四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCG=∠DCE=90°,
在△BCG和△DCE中,
,
∴△BCG≌△DCE,
∴BG=DE;
(2)存在,△BCG≌△DCE,(1)中已证明,
且△BCG和△DCE有共同顶点C,则△DCE沿C点旋转向左90°与△BCG重合.
∴BC=CD,CG=CE,∠BCG=∠DCE=90°,
在△BCG和△DCE中,
|
∴△BCG≌△DCE,
∴BG=DE;
(2)存在,△BCG≌△DCE,(1)中已证明,
且△BCG和△DCE有共同顶点C,则△DCE沿C点旋转向左90°与△BCG重合.
点评:本题考查了全等三角形的证明,考查了正方形各边相等且各内角为90°的性质,本题中求证△BCG≌△DCE是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列说法:
①直径不是弦;
②相等的弦所对的弧相等;
③在同圆或等圆中,优弧一定比劣弧长;
④同一条弦所对的两条弧是等弧.
其中正确的个数有( )
①直径不是弦;
②相等的弦所对的弧相等;
③在同圆或等圆中,优弧一定比劣弧长;
④同一条弦所对的两条弧是等弧.
其中正确的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
在等腰△ABC中,∠A的相邻外角是70°,则∠B为( )
| A、70° | B、35° |
| C、110°或35° | D、110° |
 已知:如图,△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,点E是BC上一点,且BD=BE.求∠DEC的度数.
已知:如图,△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,点E是BC上一点,且BD=BE.求∠DEC的度数. 操作题
操作题