题目内容
4．
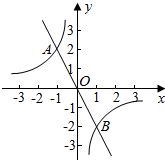如图，正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A（-1，2）、B（1，-2）两点，若y1＞y2，则x的取值范围是为（ ）| A． | x＜-1或x＞1 | B． | x＜-1或0＜x＜1 | C． | -1＜x＜0或0＜x＜1 | D． | -1＜x＜0或x＞1 |
分析 先考虑临界位置：当x=-1或x=1时y1=y2．由于x≠0，故可分x＜-1、-1＜x＜0、0＜x＜1、x＞1四种情况讨论，然后只需结合图象就可解决问题．
解答 解：如图，
结合图象可得：
①当x＜-1时，y1＞y2；②当-1＜x＜0时，y1＜y2；
③当0＜x＜1时，y1＞y2；④当x＞1时，y1＜y2．
综上所述：若y1＞y2，则x＜-1或0＜x＜1．
故选B．
点评 本题考查了有关反比例函数与一次函数交点问题，通过数形结合得到自变量的取值范围，是很重要的一种解题方法，应熟练掌握这种方法．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
12．现在网购越来越多地成为人们的一种消费方式，在2014年的“双11”网上促销活动中天猫和淘宝的支付交易额突破57000 000 000元，将数字57000 000 000用科学记数法表示为（ ）
| A． | 5.7×109 | B． | 5.7×1010 | C． | 0.57×1011 | D． | 57×109 |
9．某油箱容量为60 L的汽车，加满汽油后行驶了100 km时，油箱中的汽油大约消耗了$\frac{1}{5}$，如果加满汽油后汽车行驶的路程为x km，油箱中剩油量为y L，则y与x之间的函数解析式和自变量取值范围分别是（ ）
| A． | y=0.12x，x＞0 | B． | y=60-0.12x，x＞0 | ||
| C． | y=0.12x，0≤x≤500 | D． | y=60-0.12x，0≤x≤500 |
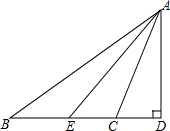如图，△ABC中，AD是高，AE是角平分线，若∠ACB=110°，∠ABC=30°，求∠CAD和∠DAE的度数．
13．
如图，⊙O是△ABC的外接圆，已知∠OAB=40°，则∠ACB为（ ）
如图，⊙O是△ABC的外接圆，已知∠OAB=40°，则∠ACB为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
