题目内容
16.已知函数y=2x2a+b+a+2b是正比例函数,则a=$\frac{2}{3}$,b=-$\frac{1}{3}$.分析 根据正比例函数的定义可得关于a和b的方程,解出即可.
解答 解:根据题意可得:2a+b=1,a+2b=0,
解得:a=$\frac{2}{3}$,b=-$\frac{1}{3}$.
故答案为:$\frac{2}{3}$;-$\frac{1}{3}$.
点评 此题考查正比例函数的定义,解题关键是掌握正比例函数的定义条件:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | 23+26=29 | B. | 23-24=2-1 | C. | 23×23=29 | D. | 24÷22=22 |
4.$\frac{1}{5}$的倒数是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
4.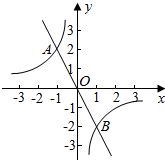 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
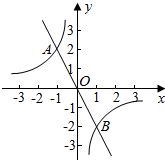 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )| A. | x<-1或x>1 | B. | x<-1或0<x<1 | C. | -1<x<0或0<x<1 | D. | -1<x<0或x>1 |
8.4的相反数是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | ±4 |