题目内容
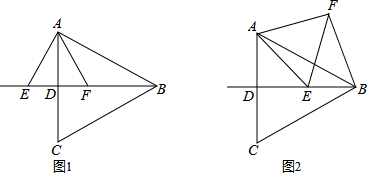
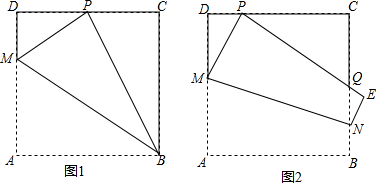
14.如图,已知△ABC为等边三角形,∠ABC的平分线BD交AC于点D,E是射线BD上的动点,以AE为边在直线AE的右侧作等边△AEF,连接EF.(1)如图①,当点F在BD上时,求证:FB=FE;
(2)如图②,当点F不在BD上时,(1)的结论是否成立?说明理由.
分析 (1)利用等边三角形的性质以及等腰三角形的判定解答即可;
(2)过点F作EG⊥AB,证得△ADE≌△AFG,结合直角三角形中30度的角所对的直角边是斜边的一半解决问题.
解答 证明:(1)∵△AEF为等边三角形,
∴AE=EF=AF,∠AFE=60°,
∵△ABC为等边三角形,∠ABC的平分线BD交AC于点D,
∴∠ABD=30°,∠AFE=∠ABD+∠FAB,
∴∠FAB=60°-30°=30°,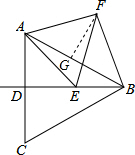
∴∠ABD=∠FAB,
∴FB=AF,
∴FB=FE;
(2)过点F作FG⊥AB于G,
∵△ABC,△AEF为等边三角形,
∴AF=AE,∠CAB=∠EAF=60°,
∴∠CAB-∠EAB=∠EAF-∠EAB,
∴∠DAE=∠BAF,
在△ADE与△AGF中,$\left\{\begin{array}{l}{∠ADE=∠AGF}\\{∠DAE=∠GAF}\\{AE=AF}\end{array}\right.$,
∴△ADE≌△AGF,
∴AG=AD,
∵AD=$\frac{1}{2}$AB,
∴AG=$\frac{1}{2}$AB,
∴AF=BF,
∴FB=FE.
点评 本题考查了等边三角形的性质,三角形全等的判定与性质,等腰三角形的判定与性质,正确的作出辅助线是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.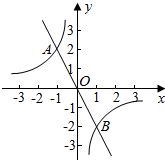 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
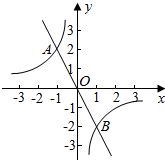 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,2)、B(1,-2)两点,若y1>y2,则x的取值范围是为( )| A. | x<-1或x>1 | B. | x<-1或0<x<1 | C. | -1<x<0或0<x<1 | D. | -1<x<0或x>1 |
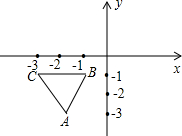 在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$).
在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$).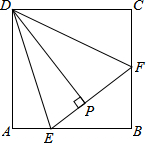 如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.
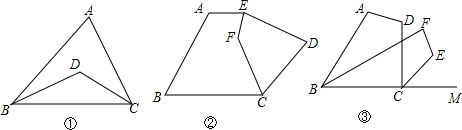
如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.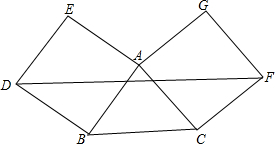 如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC.
如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC.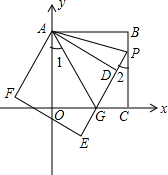 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.