题目内容
9.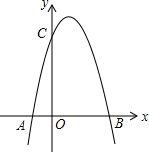 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
分析 (1)首先求得AB,得出OC,求得点C的坐标;
(2)利用待定系数法求的函数解析式,进一步利用顶点坐标公式求得最值即可.
解答 解:(1)∵A(-1,0)、B(3,0),
∴AO=1,OB=3,即AB=AO+OB=1+3=4.
∴OC=4,即点C的坐标为(0,4).
(2)设图象经过A、C、B三点的二次函数的解析式为y=ax2+bx+c,把A、C、B三点的坐标分别代入上式,
得$\left\{\begin{array}{l}a-b+c=0\\ 9a+3b+c=0\\ c=4\end{array}\right.$,
解得a=-$\frac{4}{3}$,b=$\frac{8}{3}$x,c=4,
∴所求的二次函数解析式为y=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4.
∵点A、B的坐标分别为点A(-1,0)、B(3,0),
∴线段AB的中点坐标为(1,0),即抛物线的对称轴为直线x=1.
∵a=-$\frac{4}{3}$<0,
∴当x=1时,y有最大值y=-$\frac{4}{3}$+$\frac{8}{3}$+4=$\frac{16}{3}$.
点评 本题考查了用待定系数法求二次函数的解析式,求得三点的坐标,掌握待定系数法的方法与步骤是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.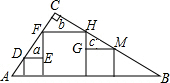 如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )
如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )
 如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )
如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )| A. | a+c=b | B. | ac=b2 | C. | a2+c2=b2 | D. | $\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a}$ |
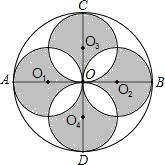 如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32.
如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32.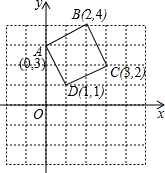 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点的坐标为(4,0);△DCB扫过的面积为$\frac{5}{2}$π+$\frac{5}{2}$.
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点的坐标为(4,0);△DCB扫过的面积为$\frac{5}{2}$π+$\frac{5}{2}$. 如图,∠ABC与∠ACB的平分线交于I,若∠ABC+∠ACB=130°,则∠BIC=115°.
如图,∠ABC与∠ACB的平分线交于I,若∠ABC+∠ACB=130°,则∠BIC=115°.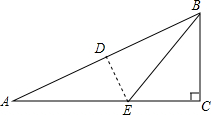 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12.
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12.