题目内容
20.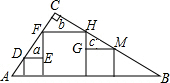 如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )
如图,在Rt△ABC(∠C=90°)内有边长分别为a、b、c的三个正方形,下列结论一定成立的是( )| A. | a+c=b | B. | ac=b2 | C. | a2+c2=b2 | D. | $\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a}$ |
分析 因为Rt△ABC内有边长分别为a、b、c的三个正方形,所以图中三角形都相似,且与a、b、c关系密切的是△DEF和△HGM,只要它们相似即可得出所求的结论.
解答 解:∵DE∥AB∥GM,
∴∠FDE=∠A,∠GMH=∠B;
又∵∠A+∠B=90°,∠FDE+∠DFE=90°,∠HMG+∠GHM=90°;
∴∠FDE=∠MHG,∠DFE=∠HMH;
∴△DEF∽△HGM,
∴$\frac{DE}{HG}=\frac{EF}{GM}$,
∴$\frac{a}{b-c}$=$\frac{b-c}{c}$,
∴ac=(b-c)(b-a)
∴b2=ab+bc=b(a+c),
∴b=a+c.
故选A.
点评 此题考查了相似三角形的判定和性质,直角三角形的性质,正方形的性质,熟练掌握三角形的判定和性质定理是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11.如表有六张卡片,卡片正面分别写有六个数字,背面分别写有六个字母.
将卡片正面的数由大到小排列,然后将卡片翻转,卡片上的字母组成的单词是thanks.
| 正面 | -(-1) | |-2| | (-1)3 | 0 | -3 | +5 |
| 背面 | a | h | k | n | s | t |
15.三角形的内心是( )
| A. | 三条中线的交点 | B. | 三个内角的角平分线的交点 | ||
| C. | 三条边的垂直平分线的交点 | D. | 三条高的交点 |
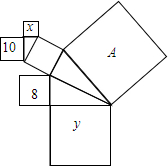 如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19.
如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19. 某居民小区有一块空地,其平面如图所示(图中各角均为直角),根据图中的数据,可求得空地的周长等于26m.
某居民小区有一块空地,其平面如图所示(图中各角均为直角),根据图中的数据,可求得空地的周长等于26m.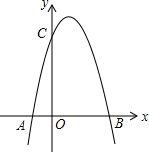 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.