题目内容
19.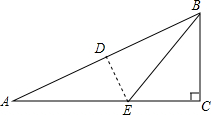 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12.
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12.
分析 先求得AE=13,然后由翻折的性质可知BE=13,最后在Rt△BCE中由勾股定理求得BC的长即可.
解答 解:∵AC=18,EC=5,
∴AE=13.
由翻折的性质可知:BE=AE=13.
在Rt△EBC中,由勾股定理得:BE2=EC2+BC2.
∴BC=$\sqrt{B{E}^{2}-E{C}^{2}}=\sqrt{1{3}^{2}-{5}^{2}}$=12.
故答案为:12.
点评 本题主要考查的是翻折的性质、勾股定理的应用,利用翻折的性质求得BE=13是解题的关键.

练习册系列答案
相关题目
4.下列各组数中,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,1,2 | C. | 8,15,17 | D. | 5,12,23 |
9.下列说法正确的是( )
| A. | 延长射线OP | B. | 延长直线CD | C. | 延长线段CD | D. | 反向延长直线DC |
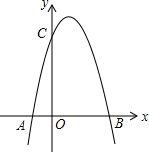 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm. 如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).
如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).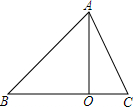 如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )
如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )