题目内容
19．若a＜$\sqrt{13}$＜b，且a、b为连续正整数，则（a+b）2=49．分析 首先得出3＜$\sqrt{13}$＜4，进而得出a，b的值，即可得出答案．
解答 解：∵a＜$\sqrt{13}$＜b，且a、b为连续正整数，
∴3＜$\sqrt{13}$＜4，则a=3，b=4，
故（a+b）2=（3+4）2=49．
故答案为：49．
点评 此题主要考查了估计无理数大小，正确得出a，b的值是解题关键．
练习册系列答案
相关题目
4．以下列数组为边长，能构成直角三角形的是（ ）
| A． | 2，3，4 | B． | 1.3，1.4，1.5 | C． | $\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$ | D． | 0.3，0.4，0.5 |
11．如表有六张卡片，卡片正面分别写有六个数字，背面分别写有六个字母．
将卡片正面的数由大到小排列，然后将卡片翻转，卡片上的字母组成的单词是thanks．
| 正面 | -（-1） | |-2| | （-1）3 | 0 | -3 | +5 |
| 背面 | a | h | k | n | s | t |
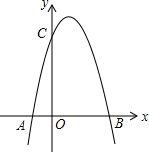如图，一个二次函数的图象经过点A、C、B三点，点A的坐标为（-1，0），点B的坐标为（3，0），点C在y轴的正半轴上，且AB=OC．