题目内容
2.观察下列等式$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
(1)直接写出$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=$\frac{3}{4}$
(2)求$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{9×10}$的值(要求写出过程)
(3)猜想并写出:$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
(4)直接写出下式的计算结果:
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$=$\frac{2006}{2007}$.
分析 (1)(2)根据已知等式解答即可;
(3)根据已知等式可得第n个等式为$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$;
(4)根据规律计算即可.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}=\frac{3}{4}$;
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{9×10}$
=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{9}-\frac{1}{10}$
=$\frac{9}{10}$;
(3)$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$;
(4)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2006}-\frac{1}{2007}=\frac{2006}{2007}$;
故答案为:$\frac{3}{4};\frac{1}{n}-\frac{1}{n+1};\frac{2006}{2007}$
点评 本题主要考查分式的混合运算,熟练掌握分式的混合运算法则是解题的关键.

练习册系列答案
相关题目
10.设a、b互为相反数,c、d互为倒数,则2013(a+b)-cd的值是( )
| A. | 2013 | B. | 0 | C. | -1 | D. | 1 |
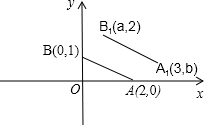 如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至点A1B1,那么a-b=0.
如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至点A1B1,那么a-b=0.