题目内容

7．若关于x的一元二次方程x2-3x+k=0有两个不相等的实数根，且满足1-k＜$\frac{k}{2}$，求k的正整数解．

分析 首先根据一元二次方程x2-3x+k=0有两个不相等的实数根，求出k的取值范围，再解一元一次不等式组即可．

解答 解：∵一元二次方程x2-3x+k=0有两个不相等的实数根，
∴△=b2-4ac=9-4k＞0，
∴k＜$\frac{9}{4}$，
∵1-k＜$\frac{k}{2}$，
∴k＞$\frac{2}{3}$，
∴$\frac{2}{3}$＜k＜$\frac{9}{4}$，
∴k的正整数解为1，2．

点评 此题考查了根的判别式以及一元一次不等式的整数解的知识，解题的关键是掌握当△＞0，方程有两个不相等的实数根．

练习册系列答案
相关题目
17．△ABC中，若∠A=2∠B，∠C=3∠B，则∠A=60°．
18．把下列各数填入相应的集合中：$\frac{1}{9}$，3，-7，-8$\frac{1}{4}$，0，5.$\stackrel{•}{6}$，15，
正数集合：{$\frac{1}{9}$，3，0，5.$\stackrel{•}{6}$，15}
负数集合：{-7，-8$\frac{1}{4}$}
整数集合：{3，-7，0，15}
分数集合：{$\frac{1}{9}$，-8$\frac{1}{4}$，5.$\stackrel{•}{6}$}．
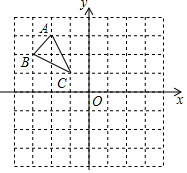15．如图，已知△ABC的三个顶点在格点上，网格上最小的正方形的边长为1．
（1）写出点A关于x轴的对称点坐标（-2，-3），写出点B关于y轴的对称点坐标（3，2）；
（2）作出与△ABC关于x轴对称的图形△A1B1C1；（不写作法）
（3）△ABC的面积=1.5（直接写出结果）．
2．观察下列等式
$\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，
（1）直接写出$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=$\frac{3}{4}$
（2）求$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{9×10}$的值（要求写出过程）
（3）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$．
（4）直接写出下式的计算结果：
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$=$\frac{2006}{2007}$．
12．若|a|=1，则a=（　　）
A．1B．-1C．1或-1D．0
19．若线段a=4cm，线段b=9cm，则线段a、b的比例中项等于6cm．
16．阅读理解：我们知道$\sqrt{3}$是无理数，而无理数是无限不循环小数，因此$\sqrt{3}$的小数部分我们不可能全部写出来，于是小张用$\sqrt{3}$-1来表示$\sqrt{3}$的小数部分，你同意小张的表示方法吗？事实上，小张的表示方法是正确的，因为1＜$\sqrt{3}$＜2，所以$\sqrt{3}$的整数部分是1，将这个数减去整数部分，差就是小数部分．请解答下列问题：
（1）填空：$\sqrt{7}$的整数部分是2，小数部分是$\sqrt{7}$-2．
（2）已知10+$\sqrt{5}$=x+y，其中x是整数，且0＜y＜1，求x-y的相反数．
17．如图所示，△ABC平移后得到了△DEF，D在AB上，若∠A=26°，∠E=74°，求∠1，∠2，∠F，∠C的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网