题目内容
15.已知点C为线段AB的中点,点D是线段CB上一点,E为DB的中点,AB=16cm,EB=3cm,则CD=( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
分析 由点C为线段AB的中点,点E为DB的中点,可以得出AC=BC=$\frac{1}{2}$AB和DB=2EB,结合图形可找出CD=CB-DB=$\frac{1}{2}$AB-2EB,代入AB=16cm,EB=3cm即可求出结果.
解答 解:画出图形,如下,
∵点C为线段AB的中点,点E为DB的中点,
∴AC=BC=$\frac{1}{2}$AB,DE=EB=$\frac{1}{2}$DB,DB=2EB,
CD=CB-DB=$\frac{1}{2}$AB-2EB,
∵AB=16cm,EB=3cm,
∴CD=16÷2-2×3=8-6=2cm.
故选A.
点评 本题考查了两点间的距离,解题的关键是画出图形,借助图形以及中点的性质找出线段间的数量关系.

练习册系列答案
相关题目
7. 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
4.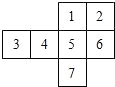 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )| A. | 1或2或3 | B. | 3或4或5 | C. | 4或5或6 | D. | 1或2或6 |
 如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数.
如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=4,则四边形MABN的面积是36.
如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=4,则四边形MABN的面积是36. 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.