题目内容
19.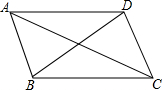 如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )
如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )| A. | ①② | B. | ③④ | C. | ②④ | D. | ①③④ |
分析 根据内错角相等两直线平行可得.
解答 解:②由∠DAC=∠BCA可得AD∥BC,
④由∠ADB=∠CBD可得AD∥BC,
故选:C.
点评 本题主要考查平行线的判定,掌握内错角相等两直线平行是解题的关键.

练习册系列答案
相关题目
14.发现思考:已知等腰三角形ABC的两边分别是方程x2-7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
涵涵的作业
| 解:x2-7x+10=0 a=1 b=-7 c=10 ∵b2-4ac=9>0 ∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ∴x1=5,x2=2 所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2. 当腰为2,底为5时,等腰三角形的三条边为2,2,5. |
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
11.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
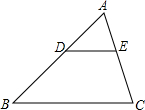 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$. 如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.
如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.