题目内容
16.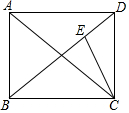 如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.
如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.
分析 过点D作DF∥AC交CE的延长线于点F,则可证得DF=CD,利用勾股定理可求得OD和OC的长,由△DEF∽△OEC可求得DE的长.
解答 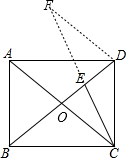 解:
解:
如图,过点D作DF∥AC交CE的延长线于点F,设AC、BD相交于点O,
∵CE平分∠ACD,
∴∠ACE=∠DCE=∠DFE,
∴DF=CD=AB=6,
∵AB=6,BC=8,
∴AC=BD=10,
∴OD=OC=5,
∵DF∥AC,
∴△DEF∽△OEC,
∴$\frac{DE}{OE}$=$\frac{DF}{OC}$,且OE=OD-DE=5-DE,
∴$\frac{DE}{5-DE}$=$\frac{6}{5}$,解得DE=$\frac{30}{11}$,
故答案为:$\frac{30}{11}$.
点评 本题主要考查矩形的性质和相似三角形的判定和性质,构造相似三角形是解题的关键.

练习册系列答案
相关题目
11.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
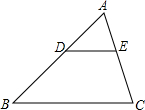 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$.
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=4,BD=6,AE=3,那么AC=$\frac{15}{2}$. 如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.
如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.