题目内容
7.综合与实践问题背景:
在一次综合与实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的研究.下面是创新小组在操作纸片过程中研究的问题,请你解决这些问题.
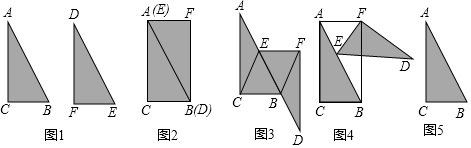
如图1,△ABC≌△DEF,其中∠ACB=90°,BC=2,AB=4.
操作与发现:
(1)如图2,创新小组将两张三角形纸片按如图示的方式放置后,经过观察发现四边形ACBF是矩形,请你证明这个结论.
操作与探究:
(2)创新小组在图2的基础上,将△DEF纸片沿AB方向平移至如图3的位置,其中点E与AB的中点重合,连接CE,BF.经过探究后发现四边形BCEF是菱形.请你证明这个结论.
(3)创新小组在图3的基础上又进行了探究,将△DEF纸片绕点E逆时针旋转至DE与BC平行的位置,如图4所示,连接AF,BF,创新小组经过观察与推理后发现四边形ACBF是矩形.请你证明这个结论.
提出问题:
(4)请你参照以上操作过程,利用图1中的两个三角形纸片,拼出新的图形,在图5中画出这个图形,标明字母,说明构图方法,并提出一个所要探究的问题,不必解答.
分析 (1)利用平行四边形的判断方法先判断出四边形ACBF是平行四边形,即可得出结论;
(2)先求出∠BAC=30°,再判断出四边形BCEF是平行四边形,进而判断出BC=CE,即可得出结论;
(3)先求出∠ABC=60°,进而判断出△AEF是等边三角形,即可判断出四边形ACBF是平行四边形,即可得出结论;
(4)先根据平移设置题目,利用相似三角形,表示出FQ,利用面积相等建立方程求解即可.
解答 解:(1)∵△ABC≌△DEF,
∴AC=DF=BF,BC=EF=AF,
在四边形ACBF中,AC=BF,BC=AF,
∴四边形ACBF是平行四边形,
∵∠ACB=90°,
∴?ACBF是矩形;
(2)在Rt△ABC中,sinA=$\frac{BC}{AB}=\frac{2}{4}$=$\frac{1}{2}$,
∴∠BAC=30°,
∵△ABC≌△DEF与平移可知,BC=EF,BC∥EF,
∴四边形BCEF是平行四边形,
∵∠ACB=90°,
∴点E与AB的中点重合,∠BAC=30°,
∴BC=CE=$\frac{1}{2}$AB,在?BCEF中,
∵BC=CE,
∴?BCEF是菱形;
(3)在Rt△ABC中,∵∠BAC+∠ABC=90°,∠BAC=30°,
∴∠ABC=60°,
∵△ABC≌△DEF,点E是AB中点,
∠BAC=30°,
∴EF=AE=BC,∠DEF=60°,
∵DE∥BC,
∴∠BED=∠ABC=60°,
∴∠AEF=180°-∠DEF-∠BED=60°,
∴AEF是等边三角形,
∴∠EAF=60°,AF=AE,
∵AE=BC,AF=BC,
∵∠EAF=∠ABC=60°,
∴AF∥BC,
在四边形ACBF中,AF=BC,AF∥BC,
∴四边形ACBF是平行四边形,
∵∠ACB=90°,
∴?ACBF是矩形;
(4)构图方法:将△DEF纸片按图所示方式放置,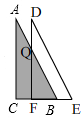 点C,F,B,E在同一条直线上,DF交AB于点Q,
点C,F,B,E在同一条直线上,DF交AB于点Q,
提问:当△BFQ的面积等于四边形CFQA的面积时,求CF的长.
解:在Rt△ABC中,BC=2,AB=4,
∴AC=2$\sqrt{3}$,
设CF=x,则BF=2-x,
由平移知,AC∥QF,
∴△BFQ∽△BCA,
∴$\frac{BF}{BC}=\frac{FQ}{AC}$,
∴$\frac{2-x}{2}=\frac{FQ}{2\sqrt{3}}$,
∴FQ=$\sqrt{3}$(2-x),
∴S△BFQ=$\frac{1}{2}$BF•FQ=$\frac{\sqrt{3}}{2}$(2-x)2,
∵△BFQ的面积等于四边形CFQA的面积,
∴S△BFQ=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$BC×AC=$\sqrt{3}$,
∴$\frac{\sqrt{3}}{2}$(2-x)2=$\sqrt{3}$,
∴x=2+$\sqrt{2}$(舍)或x=2-$\sqrt{2}$,
即:CF的长为2-$\sqrt{2}$.
点评 此题是四边形综合题,主要考查了全等三角形的判定和性质,平行四边形的判定和性质,菱形,矩形的判断和性质,等边三角形的判定和性质,相似三角形的判定和性质,解(1)的关键是判断四边形ACBF是平行四边形,解(2)的关键是判断出BE=CE,解(3)的关键是判断出△AEF是等边三角形,解(4)的关键是利用面积建立方程求解.

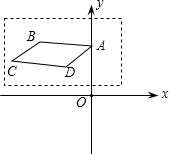 在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1).
在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1).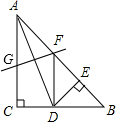 如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为4-2$\sqrt{2}$.
如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为4-2$\sqrt{2}$.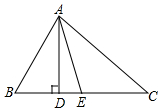 如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是34°.
如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是34°. 如图,点E、F在?ABCD的对角线AC上,且AE=CF.求证:DE=BF.
如图,点E、F在?ABCD的对角线AC上,且AE=CF.求证:DE=BF.
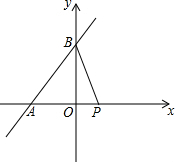 如图,直线y=$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,点P是x轴上的一个动点.
如图,直线y=$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,点P是x轴上的一个动点.