题目内容
16.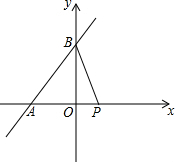 如图,直线y=$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,点P是x轴上的一个动点.
如图,直线y=$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点B,点P是x轴上的一个动点.(1)求A、B两点的坐标;
(2)当点P在x轴正半轴,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
分析 (1)根据坐标轴上点的特点即可得出结论;
(2)设出点P坐标,利用△PAB的面积建立方程求出P的坐标,最后用待定系数法求解即可;
(3)先判断出点Q在直线y=4上,再分两种情况讨论计算即可.
解答 解:(1)令x=0时,y=4,
∴B(0,4),
令y=0时,$\frac{4}{3}$x+4=0,
∴x=-3,
∴A(-3,0);
(2)设点P(m,0)(m>0),
∵A(-3,0),
∴AP=m-(-3)=m+3,
∵△APB的面积为8,
∴S△APB=$\frac{1}{2}$AP×OB=$\frac{1}{2}$(m+3)×4=8,
∴m=1,
∴P(1,0),
∵B(0,4),
∴设直线PB的解析式为y=kx+4,
∴k+4=0,
∴k=-4,
∴直线PB的解析式为y=-x+4;
(3)如图,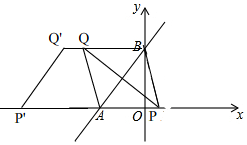
∵以A、B、P、Q为顶点的四边形是菱形,且P在x轴上,
∴BQ∥AP,
∴点Q在直线y=4上,
由(1)知,A(-3,0),B(0,4),
∴AB=5,
∵点Q在第二象限内,
∴①当AB为菱形的边时,
∴BQ'=AB=5,
∴Q'(-5,4),
②当AB为菱形的对角线时,AB,PQ互相垂直平分,
∵直线AB的解析式为y=$\frac{4}{3}$x+4,
∴直线PQ的解析式为y=-$\frac{3}{4}$x+$\frac{7}{8}$,
当y=4时,则-$\frac{3}{4}$x+$\frac{7}{8}$=4,
∴x=-$\frac{25}{6}$,
∴Q(-$\frac{25}{6}$,4),
∴满足条件的点Q的坐标为(-5,4)或(-$\frac{25}{6}$,4).
点评 此题是一次函数综合题,主要考查了待定系数法,三角形的面积公式,菱形的性质,用方程的思想解决问题是就本题的关键.

练习册系列答案
相关题目
1.某校开展“快乐阅读”活动,倡导利用课余时间阅读纸质书籍.该学校共有300名学生,随机调查了其中30名学生在活动开展的一年里阅读纸质书籍的数量,将收集的数据进行了整理,绘制的统计表如下:
请你估计该学校这一年里平均每名学生阅读纸质书籍的数量是10本(结果保留整数).
| 阅读纸质书籍的数量(本) | 3 | 7 | 11 | 15 |
| 人数 | 4 | 8 | 10 | 8 |
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{\frac{1}{3}}$ |
 解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.