题目内容
12.若关于x的不等式组$\left\{\begin{array}{l}\frac{x}{2}+a>2\\ 2x-b<3\end{array}\right.$的解集为2<x<3,则a+b的值为4.分析 分别求出每一个不等式的解集,根据不等式组的解集得出关于a、b的方程组,解之求得a、b的值即可得出答案.
解答 解:解不等式$\frac{x}{2}$+a>2,得:x>4-2a,
解不等式2x-b<3,得:x<$\frac{b+3}{2}$,
∵不等式组的解集为2<x<3,
∴$\left\{\begin{array}{l}{4-2a=2}\\{\frac{b+3}{2}=3}\end{array}\right.$,
解得:a=1,b=3,
则a+b=4
故答案为:4.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,得出关于a、b的方程组是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.某校开展“快乐阅读”活动,倡导利用课余时间阅读纸质书籍.该学校共有300名学生,随机调查了其中30名学生在活动开展的一年里阅读纸质书籍的数量,将收集的数据进行了整理,绘制的统计表如下:
请你估计该学校这一年里平均每名学生阅读纸质书籍的数量是10本(结果保留整数).
| 阅读纸质书籍的数量(本) | 3 | 7 | 11 | 15 |
| 人数 | 4 | 8 | 10 | 8 |
2.方程2x2-3x-1=0用公式法求解,先确定a,b,c的值,正确的是( )
| A. | a=2,b=-3,c=-1 | B. | a=-2,b=3,c=1 | C. | a=-2,b=-3,c=-1 | D. | a=2,b=3,c=-1 |

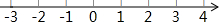 解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.