题目内容
13.已知x>y>z,且x+y+z=0,下列不等式一定成立的是( )| A. | xy>yz | B. | xz>yz | C. | xy>xz | D. | xy2>zy2 |
分析 根据已知x>y>z和x+y+z=0得出x>0,z<0,再根据不等式的性质逐个判断即可.
解答 解:∵x>y>z,且x+y+z=0,
∴x>0,z<0,
∵y>z,
A、根据已知不能确定y的符号,
根据x>z不一定能推出xy>yz,故本选项不符合题意;
B、∵x>y,z<0,
∴xz<yz,故本选项不符合题意;
C、∵y>z,x>0,
∴xy>xz,故本选项符合题意;
D、根据x>z不能得出xy2>zy2(当y=0时不对),故本选项不符合题意;
故选C.
∴两边都乘以x得:xy>xz,
点评 本题考查了不等式的基本性质,能根据不等式的性质进行变形是解此题的关键.

练习册系列答案
相关题目
3.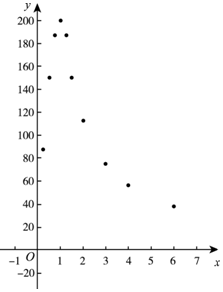 阅读下列材料:
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
 阅读下列材料:
阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
5.不等式-2x≥8的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
2.根据下列表述,能确定位置的是( )
| A. | 东经116°,北纬42° | B. | 红星大桥南 | ||
| C. | 北偏东30° | D. | 太平洋影院第2排 |
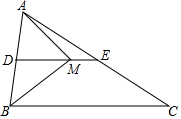 在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.
在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8. 如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=3.
如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=3.


