题目内容
4.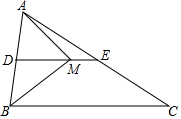 在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.
在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=$\frac{1}{3}$DM.当AM⊥BM时,则BC的长为8.
分析 根据直角三角形的性质求出DM,根据题意求出DE,根据三角形中位线定理计算即可.
解答 解:∵AM⊥BM,点D是AB的中点,
∴DM=$\frac{1}{2}$AB=3,
∵ME=$\frac{1}{3}$DM,
∴ME=1,
∴DE=DM+ME=4,
∵D是AB的中点,DE∥BC,
∴BC=2DE=8,
故答案为:8.
点评 本题考查的是三角形的中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
14.关于x的一元二次方程(a+1)x2-x+a2-2a-2=0,有一个根是1,则a=( )
| A. | -1 | B. | 2 | C. | 2或-1 | D. | -2或1 |
12. 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.三角形的两边a、b的夹角为60°且满足方程x2-3$\sqrt{2}$x+4=0,则第三边的长是( )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
13.已知x>y>z,且x+y+z=0,下列不等式一定成立的是( )
| A. | xy>yz | B. | xz>yz | C. | xy>xz | D. | xy2>zy2 |

 中国讲究五谷丰登,六畜兴旺.如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后,则与“牛”相对的是( )
中国讲究五谷丰登,六畜兴旺.如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后,则与“牛”相对的是( )