题目内容
3.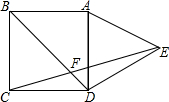 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
分析 由于四边形ABCD是正方形,△ADE是正三角形,由此可以得到CD=DE,接着利用正方形和正三角形的内角的性质即可求解.
解答 解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
又∵△ADE是正三角形,
∴CD=DE,∠ADE=60°,
∴△CDE是等腰三角形,∠CDE=90°+60°=150°,
∴∠ECD=∠DEC=15°,
∵∠BDC=45°,
∴∠CFD=180°-15°-45°=120°,
∴∠BFC=60°,
故选D
点评 此题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
11.解不等式组$\left\{\begin{array}{l}{\frac{1+2x}{3}>x-1}\\{4(x-1)≥3x-4}\end{array}\right.$,并将解集在数轴上表示出来.
18.下列由线段a,b,c组成的三角形,不是直角三形的是( )
| A. | a=40,b=50,c=60 | B. | a=7,b=24,c=25 | C. | a=$\sqrt{41}$,b=4,c=5 | D. | a=$\frac{5}{4}$,b=1,c=$\frac{3}{4}$ |
13.一次函数y=-x+2图象经过( )象限.
| A. | 一、二、三 | B. | 一、二、四 | C. | 一、三、四 | D. | 二、三、四 |
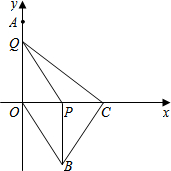 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.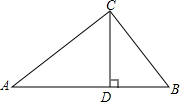 已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.
已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.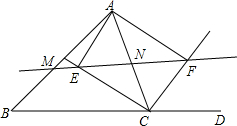 已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.