题目内容
8.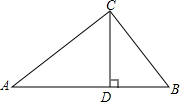 已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.
已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.(1)分别求出DC、AD、AB的长;
(2)猜想:△ABC是什么特殊三角形,并证明你的猜想.
分析 (1)在Rt△CDB中,根据勾股定理得DC,在Rt△ACD中,根据勾股定理得AD,再根据AB=AD+BD即可求解;
(2)根据勾股定理的逆定理即可得到△ABC是直角三角形.
解答 解:(1)∵CD⊥AB于D点,
∴∠CDB=∠CDA=90°,
在Rt△CDB中,BC=3,DB=$\frac{9}{5}$,
根据勾股定理得DC=$\sqrt{{3}^{2}-(\frac{9}{5})^{2}}$=$\frac{12}{5}$,
在Rt△ACD中,AC=4,DC=$\frac{12}{5}$,
根据勾股定理得AD=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∴AB=AD+BD=$\frac{16}{5}$+$\frac{9}{5}$=5;
(2)猜想:△ABC是直角三角形.
∵在△ABC中,AC=4,BC=3,AB=5,
∴AC2+BC2=42+32=52=AB2,
∴△ABC是直角三角形.
点评 考查了勾股定理的逆定理,勾股定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
16.下列运算和化简,不正确的是( )
| A. | $\sqrt{{{0.5}^2}}$=0.5 | B. | $\sqrt{\frac{4}{3}}=\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{8}×\sqrt{\frac{1}{2}}=2$ | D. | ${(-7\sqrt{\frac{2}{7}})^2}=7\frac{2}{7}$ |
3.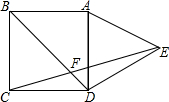 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
20.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{0.75}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{22}$ | D. | $\sqrt{63}$ |
17.下列说法中正确的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 同位角相等 | |
| C. | 垂直于同一条直线的两条直线互相平行 | |
| D. | 对顶角相等 |
18.不等式x-2≤0的解集是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
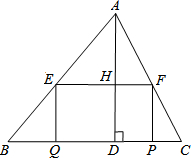 如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.
如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.