题目内容
14.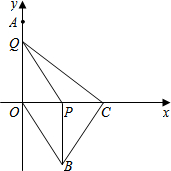 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.(1)求点B、C的坐标;(用含t的代数式表示)
(2)当t=1时,在平面内存在一点D,使得以点Q、B、C、D为顶点的四边形是平行四边形,直接写出此时点D的坐标.
(3)当∠QPC=90°+∠α(其中α为△PBC的一个内角)时,求t的值.
分析 (1)根据平行四边形的性质得出QO=PB,进而得出点B,C的坐标即可;
(2)根据平行四边形的性质列出点D的三种情况得出坐标即可;
(3)根据α为△PBC的一个内角的两种情况进行分析解答即可.
解答 解:(1)设点P运动的时间为t,
可得:OP=2t,QO=OA-AQ=4-t,
所以点B的坐标为(2t,t-4),点C的坐标为(2+2t,0);
(2)要使以点Q、B、C、D为顶点的四边形是平行四边形,
则可得点D的坐标有三种情况,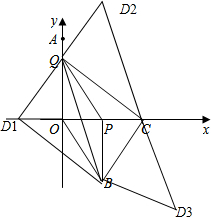
当QD∥BC,当t=1时,OD1=PC=2,故点D1的坐标为(-2,0);
当QD∥BC,当t=1时,点B的坐标为(2,-3),3+3=6,故可得点D2的坐标为(2,6);
当QB∥DC,当t=1时,点C的坐标为(4,0),故可得点D3的坐标为(6,-6);
(3)因为当∠QPC=90°+∠α(其中α为△PBC的一个内角)时,
可得:当∠PCB=α时,△QPO≌△PCB,OP=PC,即2t=2,解得:t=1;
当∠PBC=α时,△QPO~△PCB,可得:$\frac{PC}{BP}=\frac{QO}{OP}$,
即:$\frac{2}{4-t}=\frac{4-t}{2t}$,
解得:${t}_{1}=6-2\sqrt{5},{t}_{2}=6+2\sqrt{5}$(舍去).
点评 此题考查四边形的综合题,关键是根据平行四边形的性质进行分析,结合相似三角形和坐标的问题进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )| A. | 50° | B. | 45° | C. | 40° | D. | 25° |
3.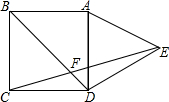 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
 如图,△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB,垂足为E,则∠ADE的度数是60°.
如图,△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB,垂足为E,则∠ADE的度数是60°.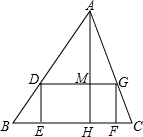 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,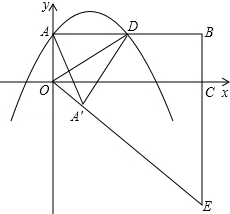 如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D