题目内容
15.已知4x+y=3,且y≤7,则x的取值范围是x≥-1.分析 先根据4x+y=3用x表示出y,再根据y≤7求出x的取值范围即可.
解答 解:∵4x+y=3,
∴y=3-4x.
∵y≤7,
∴3-4x≤7,解得x≥-1.
故答案为:x≥-1.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
6. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )| A. | 50° | B. | 45° | C. | 40° | D. | 25° |
3.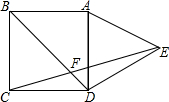 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
20.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{0.75}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{22}$ | D. | $\sqrt{63}$ |
5.求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,S=22015-1,我们把这种求和的方法叫错位相加减,仿照上述的思路方法,计算出1+5+52+53+…+52014的值为( )
| A. | 52014-1 | B. | 52015-1 | C. | $\frac{{5}^{2015}-1}{4}$ | D. | $\frac{{5}^{2014}-1}{4}$ |
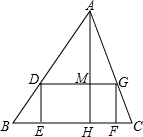 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,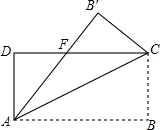 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在点B′处,则重叠部分△APC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在点B′处,则重叠部分△APC的面积为( )