题目内容
11.解不等式组$\left\{\begin{array}{l}{\frac{1+2x}{3}>x-1}\\{4(x-1)≥3x-4}\end{array}\right.$,并将解集在数轴上表示出来.分析 求出两个不等式的解集,根据找不等式组解集的规律找出公共部分即可.
解答 解:解不等式①得:x<4,
解不等式②得:x≥0,
所以不等式组的解集为:0≤x<4,
在数轴上表示为:
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集的应用,关键是能求出不等式组的解集.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,如果∠A=50°,则∠DCB=( )| A. | 50° | B. | 45° | C. | 40° | D. | 25° |
16.下列运算和化简,不正确的是( )
| A. | $\sqrt{{{0.5}^2}}$=0.5 | B. | $\sqrt{\frac{4}{3}}=\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{8}×\sqrt{\frac{1}{2}}=2$ | D. | ${(-7\sqrt{\frac{2}{7}})^2}=7\frac{2}{7}$ |
3.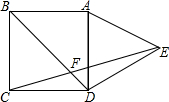 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
20.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{0.75}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{22}$ | D. | $\sqrt{63}$ |
1. 如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的边AC为( )
如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的边AC为( )
 如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的边AC为( )
如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的边AC为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 10 |
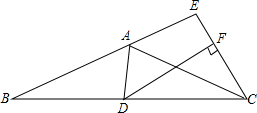 如图,等腰△ABC中,AB=AC,∠BAD=60°,将射线CA绕点C顺时针旋转交BA的延长线于点E,且∠ACE=$\frac{1}{2}$∠DAC,过点D作DF⊥CE于点F交AC于点G,若AB=5,AD=2,则AE=3.
如图,等腰△ABC中,AB=AC,∠BAD=60°,将射线CA绕点C顺时针旋转交BA的延长线于点E,且∠ACE=$\frac{1}{2}$∠DAC,过点D作DF⊥CE于点F交AC于点G,若AB=5,AD=2,则AE=3.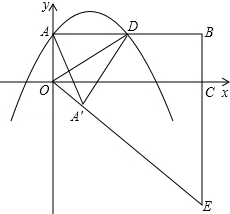 如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D