题目内容
已知△ABC中,∠A为最小角,∠B为最大角,且2∠B=5∠A,则∠B的最大值为 .
考点:三角形内角和定理
专题:
分析:由2∠B=5∠A,得∠B=
∠A,根据三角形内角和定理得∠C=180°-∠A-∠B=180°-
∠A;根据题意有∠A≤∠C≤∠B,则∠A≤180°-
∠A,和180°-
∠A≤
∠A,解两个不等式得30°≤∠A≤40°,而∠A=
∠B,得到∠B的范围,进而得出结论.
| 5 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
解答:解:∵2∠B=5∠A,即∠B=
∠A,
∴∠C=180°-∠A-∠B=180°-
∠A,
又∵∠A≤∠C≤∠B,
∴∠A≤180°-
∠A,
解得∠A≤40°;
又∵180°-
∠A≤
∠A,
解得∠A≥30°,
∴30°≤∠A≤40°,即30°≤
∠B≤40°,
∴75°≤∠B≤100°.
故答案为:100°.
| 5 |
| 2 |
∴∠C=180°-∠A-∠B=180°-
| 7 |
| 2 |
又∵∠A≤∠C≤∠B,
∴∠A≤180°-
| 7 |
| 2 |
解得∠A≤40°;
又∵180°-
| 7 |
| 2 |
| 5 |
| 2 |
解得∠A≥30°,
∴30°≤∠A≤40°,即30°≤
| 2 |
| 5 |
∴75°≤∠B≤100°.
故答案为:100°.
点评:本题考查了三角形的内角和定理,熟知三角形的内角和为180°是解答此题的关键.

练习册系列答案
相关题目
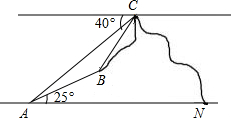 如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
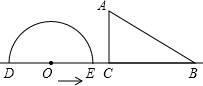 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.