题目内容
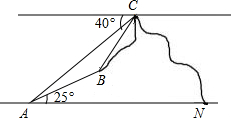 如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设AB=2a,则BC=3a,作BE⊥MN、CD⊥MN、BF⊥CD分别于点E、D、F,利用三角函数求得CD和AD的长,则tan∠CAD的值即可求解,进而求得∠CAD.
解答: 解:设AB=2a,则BC=3a,作BE⊥MN、CD⊥MN、BF⊥CD分别于点E、D、F.
解:设AB=2a,则BC=3a,作BE⊥MN、CD⊥MN、BF⊥CD分别于点E、D、F.
在直角△ABE中,BE=AB•sin∠BAE=2a•sin25°≈0.85a,
AE=AB•cos∠BAE=2a•cos25°≈1.81a.
在直角△BCF中,CF=BC•sin∠CBF=3a•sin40°≈1.93a,
BF=BC•cos∠CBF=3a•cos40°≈2.30a,
则CD=CF+BE=1.93a+0.85a=2.78am
AD=AE+BF=1.81a+2.30a=4.11a,
则tan∠CAD=
=
≈0.676,
则∠CAD≈34.1°.
即由A处测得C处的仰角是34.1°.
 解:设AB=2a,则BC=3a,作BE⊥MN、CD⊥MN、BF⊥CD分别于点E、D、F.
解:设AB=2a,则BC=3a,作BE⊥MN、CD⊥MN、BF⊥CD分别于点E、D、F.在直角△ABE中,BE=AB•sin∠BAE=2a•sin25°≈0.85a,
AE=AB•cos∠BAE=2a•cos25°≈1.81a.
在直角△BCF中,CF=BC•sin∠CBF=3a•sin40°≈1.93a,
BF=BC•cos∠CBF=3a•cos40°≈2.30a,
则CD=CF+BE=1.93a+0.85a=2.78am
AD=AE+BF=1.81a+2.30a=4.11a,
则tan∠CAD=
| CD |
| AD |
| 2.78a |
| 4.11a |
则∠CAD≈34.1°.
即由A处测得C处的仰角是34.1°.
点评:本题考查了解直角三角形,正确理解方向角的定义,理解直角三角形中的边和角的关系是关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
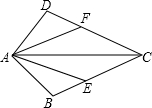 已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.
已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.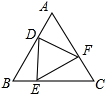 如图,等边△ABC中,DE⊥BC,DF⊥AB,EF⊥AC,说明△DEF为等边三角形.
如图,等边△ABC中,DE⊥BC,DF⊥AB,EF⊥AC,说明△DEF为等边三角形.