题目内容
11.在△ABC中,AB=20,AC=13,BC边上的高AD=12,则△ABC的周长为44或54.分析 已知三角形两边的长和第三边的高,未明确这个三角形为钝角还是锐角三角形,所以需分情况讨论,即∠ABC是钝角还是锐角,然后利用勾股定理求解.
解答 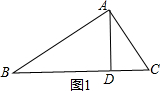 解:如图1,△ABC中,AB=20,AC=13,BC边上高AD=12,
解:如图1,△ABC中,AB=20,AC=13,BC边上高AD=12,
在Rt△ABD中AB=20,AD=12,
由勾股定理得,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=16,
在Rt△ADC中AC=13,AD=12,
由勾股定理得,DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=5,
则BC的长为BD+DC=9+16=21,
△ABC的周长为:13+20+21=54,
如图2,同(1)的作法相同,BC=11,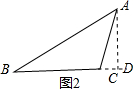
△ABC的周长为:13+20+11=44,
故答案为:44或54.
点评 本题主要考查了勾股定理,解决问题的关键是在直角三角形中用勾股定理求得线段的长.当已知条件中没有明确角的大小时,要注意讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.当x取什么值时,$\sqrt{9x+1}$+1取值最小,这个最小值是多少?( )
| A. | 当x=0时,最小值是2 | B. | .当x=-$\frac{1}{9}$时,最小值是1 | ||
| C. | .当x=$\frac{1}{9}$时,最小值是1 | D. | .当x=-$\frac{1}{9}$时,最小值是2 |
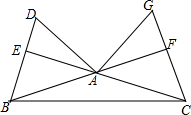 已知:如图:在钝角△ABC中,BE、CF分别是AC、AB两边上的高,在射线BE上截取BD=AC,在射线CF的延长线上截取CG=AB,连结AD、AG.
已知:如图:在钝角△ABC中,BE、CF分别是AC、AB两边上的高,在射线BE上截取BD=AC,在射线CF的延长线上截取CG=AB,连结AD、AG. 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.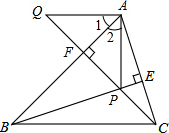 已知:如图,BE,CF是△ABC的高,且BP=AC,CQ=AB.
已知:如图,BE,CF是△ABC的高,且BP=AC,CQ=AB.