题目内容
1.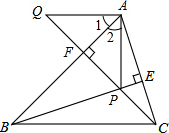 已知:如图,BE,CF是△ABC的高,且BP=AC,CQ=AB.
已知:如图,BE,CF是△ABC的高,且BP=AC,CQ=AB.(1)求证:∠Q=∠2;
(2)求证:AP⊥AQ.
分析 (1)由△ACQ≌△PBA,(SAS)推出AP=AQ,∠Q=∠BAP,由∠Q+∠QAB=90°,推出∠BAP+∠QAB=90°,推出AP⊥AQ,再利用等角的余角相等即可证明;
(2)见(1)中证明;
解答 解:(1)∵CF、BE是△ABC的高,
∴∠ABE+∠BAE=90°,∠ACQ+∠BAE=90°,
∴∠ABE=∠ACQ,
∵在△ACQ和△PBA中,
$\left\{\begin{array}{l}{BP=AC}\\{∠ABE=∠ACQ}\\{CQ=AB}\end{array}\right.$,
∴△ACQ≌△PBA,(SAS)
∴AP=AQ,∠Q=∠BAP,
∵∠Q+∠QAB=90°,
∴∠BAP+∠QAB=90°,
∴AP⊥AQ,
∴∠2+∠APF=90°,∠Q+∠APF=90°,
∴∠Q=∠2.
(2)见(1)中证明.
点评 本题考查全等三角形的判定和性质、等角的余角相等等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.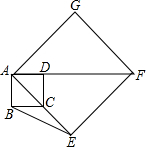 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |
11.已知mn≠1,且5m2+2010m+9=0,9n2+2010n+5=0,则$\frac{m}{n}$的值为( )
| A. | -402 | B. | $\frac{5}{9}$ | C. | $\frac{9}{5}$ | D. | $\frac{670}{3}$ |

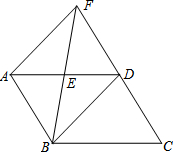 如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°.
如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°. 若画图并填空:
若画图并填空: