题目内容
3. 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
分析 根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
解答 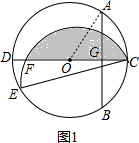 解:连接AO,如右图1所示,
解:连接AO,如右图1所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG=$\frac{1}{2}$=4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=-1(舍去),
∴5k=5,
即⊙O的半径是5;
如图2所示,将阴影部分沿CE翻折,点F的对应点为M,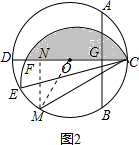
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MO•sin60°=5×$\frac{\sqrt{3}}{2}$,
∴S阴影=S扇形OMC-S△OMC=$\frac{120×π×{5}^{2}}{360}$-$\frac{25\sqrt{3}}{4}$=$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$,
即图中阴影部分的面积是:$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
故答案为:5,$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
点评 本题考查垂径定理、扇形的面积、翻折变换,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.已知4x2+8(n+1)x+16n是一个关于x的完全平方式,则常数n的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
8.学校要举行“诗词大会”,七、八年级每班选拔一人参加最终的决赛.七年级一班通过层层选拔,最后要从A同学和B同学中选择一人参加学校的比赛,语文老师给这两位同学进行了10次诗词相关知识的测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,达到9分或10分为优秀.成绩如表1所示,并制作了成绩分析表(表2)
表1
表2
(1)在表2中,a=8,b=8,c=10,d=2.8,e=90%,f=30%;
(2)有人说B同学成绩比A同学成绩好;但也有人坚定认为A同学成绩比B同学成绩好.请你分别给出支持A同学或支持B同学的理由.
表1
| A同学 | 5 | 8 | 8 | 9 | 8 | 10 | 9 | 8 | 8 | 5 |
| B同学 | 10 | 7 | 7 | 9 | 10 | 5 | 8 | 6 | 10 | 8 |
| 同学 | 平均分 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
| A | 7.8 | b | 8 | 2.36 | 80% | f |
| B | a | 7 | c | d | e | 40% |
(2)有人说B同学成绩比A同学成绩好;但也有人坚定认为A同学成绩比B同学成绩好.请你分别给出支持A同学或支持B同学的理由.
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论: 如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10=-8.
如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10=-8.