题目内容
若a是不等式2x﹣1＞5的解，b不是不等式2x﹣1＞5的解，则下列结论正确的是（ ）
A. a＞b B. a≥b C. a＜b D. a≤b
A
【解析】解2x﹣1＞5得x＞3，．
a是不等式2x﹣1＞5的解则a＞3，b不是不等式2x﹣1＞5的解，则b≤3．
故a＞b．
故选A．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
(1)解不等式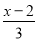
－
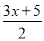≥x－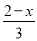
，并把它的解集在数轴上表示出来．
(2)解不等式组： 
，并把解集在数轴上表示出来．
（1）x≤－1，解集在数轴上表示见解析；（2）原不等式组无解.
【解析】试题分析：（1）根据不等式的解法，利用去分母，去括号，移项合并同类项，系数化为1，解不等式，再表示在数轴上即可；
（2）分别解两个不等式，然后求出不等式组的解集，并表示在数轴上.
试题解析：(1) 【解析】
原不等式化简为：2x－4－9x－15≥6x－4＋2x，解得x≤－1，解集在数轴上表示为：
(2... 如图所示，已知AD∥BC，要使四边形ABCD为平行四边形，需要增加的条件是________．(只需填一个你认为正确的条件即可).
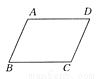
AD＝BC，或AB∥AD(答案不唯一)
【解析】【解析】
根据平行四边形的判定方法，需要增加的条件是：AD=BC或AB∥CD或∠A=∠C或∠B=∠D．故答案为：AD=BC（或AB∥CD）． 某商店先在广州以每件15元的价格购进某种商品10件，后来又到深圳以每件12.5元的价格购进同种商品40件，如果商店销售这些商品时，每件定价为x元，则会获得不少于12%的利润，用不等式表示以上问题中的不等关系，并把这个不等式变形为“x≥a”或“x≤a”的形式．
x≥14.56.
【解析】试题分析：关系式为：总售价-总进价＞总进价×12%，把相关数值代入化简即可.
试题解析：由题意得
(10＋40)x－(15×10＋12.5×40)≥(15×10＋12.5×40)×12%，
∴x≥14.56. 方程3x＝12的解有___个，不等式3x＜12的解有____个．
1 无数
【解析】解方程3x=12，可得x=4，所以方程只有一个解，解不等式3x＜12，可得x＜4，知不等式的解有无数个.
故答案为：1；无数. 如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（ ）
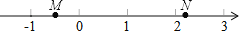
A. m+n＜0 B. 
m＜
n C. |m|
|n|＞0 D. 2+m＜2+n
D
【解析】试题分析：根据M、N两点在数轴上的位置判断出其取值范围，再对各选项进行逐一作出判断：
由M、N两点在数轴上的位置可知：-1＜M＜0，N＞2，
∵-1＜M＜0，N＞2，∴M+N＞0，故A错误.
∵M＜N，∴-M＞-N，故B错误.
∵-1＜M＜0，N＞2，∴|m|-|n|＜0，故C错误．
∵M＜N，∴2+m＜2+n，故D正确.
故选D． 已知和多边形一个内角相邻的外角与其余各内角度数总和为600°，求该多边形的边数．
边数为5或6．
【解析】分析：设多边形的边数为n,内角为x,根据多边形内角和定理得到(n－2)×180°－x＋180－x＝600，化简用含n的式子表示x,再由0＜x＜180，得到n的取值范围，结合n为正整数即可求解.
本题解析：
设边数为n，这个内角的度数为x.根据题意，得
(n－2)×180°－x＋180－x＝600.
解方程，得x＝90n－390.
∵ 0＜... 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）
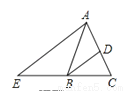
A. 40° B. 45° C. 60° D. 70°
A
【解析】根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．
【解析】
∵AE∥BD，∴∠CBD=∠E=35°，∵BD平分∠ABC，∴∠CBA=70°，∵AB=AC，
∴∠C=∠CBA=70°，∴∠BAC=180°﹣70°×2=40°．
故选A．
“点睛”考查了平行... 如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（ ）
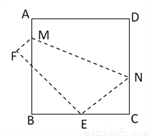
A. 3cm B. 4cm C. 5cm D. 6cm
A
【解析】分析：根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8-x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．
解答：【解析】
设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8-x）2=16+x...