题目内容
2.根据条件求二次函数的解析式(1)抛物线过(-1,-22),(0,-8),(2,8)三点;
(2)抛物线过(-1,0),(3,0),(1,-5)三点;
(3)抛物线在x轴上截得的线段长为4,且顶点坐标是(3,-2);
(4)二次函数的图象经过点(-1,0),(3,0),且最大值是3.
分析 (1)先设出抛物线的解析式为y=ax2+bx+c,再将点(-1,-22),(0,-8),(2,8)代入解析式中,即可求得抛物线的解析式;
(2)由于已知抛物线与x轴的交点坐标,则设交点式y=a(x+1)(x-3),然后把(1,-5)代入求出a的值即可.
(3)根据抛物线的对称性得到抛物线与x轴的两交点坐标为(0,0),(8,0),则可设交点式y=ax(x-8),然后把顶点坐标代入求出a即可.
(4)根据题意设抛物线解析式为y=a(x+1)(x-3),再由最大值为3求出a的值,即可确定出抛物线解析式.
解答 解:(1)设出抛物线的解析式为y=ax2+bx+c,将点(-1,-22),(0,-8),(2,8)代入解析式得:$\left\{\begin{array}{l}{a-b+c=-22}\\{c=-8}\\{4a+2b+c=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=12}\\{c=-8}\end{array}\right.$,
∴抛物线解析式为:y=-2x2+12x-8;
(2)设抛物线解析式为y=a(x+1)(x-3),
把(1,-5)代入得-4a=-5,解得a=$\frac{5}{4}$,
所以抛物线解析式为y=$\frac{5}{4}$(x+1)(x-3),即抛物线的解析式为y=$\frac{5}{4}$x2-$\frac{5}{2}$x-$\frac{15}{4}$;
(3)根据题意得抛物线的对称轴为直线x=3,
而抛物线在x轴上截得的线段长为4,
所以抛物线与x轴的两交点坐标为(1,0),(5,0),
设抛物线解析式为y=a(x-1)(x-5),
把(3,-2)代入得a•2•(-2)=-2,解得a=$\frac{1}{2}$,
所以抛物线解析式为y=$\frac{1}{2}$(x-1)(x-5),即y=$\frac{1}{2}$x2-3x+$\frac{5}{2}$.
(4)设抛物线解析式为y=a(x+1)(x-3)=ax2-2ax-3a=a(x-1)2-4a,
由最大值为3,得到-4a=3,即a=-$\frac{3}{4}$,
则抛物线解析式为y=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{9}{4}$.
点评 本题考查了待定系数法求二次函数的解析式:一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.本题的关键是利用对称性确定抛物线与x轴的交点坐标.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | 345 | B. | 357 | C. | 456 | D. | 567 |
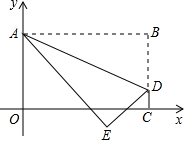 如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )
如图,将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C在x轴上,点D(3$\sqrt{5}$,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.若抛物线y=ax2-4$\sqrt{5}$ax+10(a≠0且a为常数)的顶点落在△ADE的内部,则a的取值范围是( )| A. | $\frac{2}{5}<a<\frac{13}{20}$ | B. | $\frac{2}{5}<a<\frac{11}{20}$ | C. | $\frac{11}{20}<a<\frac{3}{5}$ | D. | $\frac{3}{5}<a<\frac{13}{20}$ |

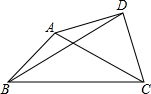 如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$.
如图四边形ABCD中,AB=4$\sqrt{2}$,BC=12,∠ABC=45°,∠ADC=90°,AD=CD,则BD=2$\sqrt{34}$. 如图,AB∥CD,∠E=60°,则∠B+∠F+∠C=240°.
如图,AB∥CD,∠E=60°,则∠B+∠F+∠C=240°.